The Effectiveness of Applying Realistic Mathematics Education Approach in Teaching Statistics in Grade 7 to Students' Mathematical Skills

Bui Phuong Uyen 1 ; Duong Huu Tong2* ; Nguyen Phu Loc3 ; Le Nguyen Phuoc Thanh4

1,2,3School of Education, Can Tho University, Can Tho City, Vietnam.
4 Tang Nhon Phu B Junior School, Ho Chi Minh City, Vietnam.

Abstract

The research was carried out to verify the effectiveness of applying Realistic Mathematics Education (RME) on the development of skills required by students in statistical content in grade 7. For achieving research objectives, the pedagogical experiment was conducted in the form of intrinsic legalization for forty-eight 7th-grade students at Tang Phu Nhan B Junior School, District 9, Ho Chi Minh City, Vietnam. Accordingly, data on pre-test results, study sheets, post-test, and student learning performance were collected and analyzed qualitatively. The results were assessed based on the criteria corresponding to the required skills for the statistical content, including the criteria for data collection, classification, and representation according to the given criteria for the skill, data collection, and organization capabilities; simple problem formation and problem-solving criteria arise from the existing statistical figures and charts for data analysis and processing skills. The primary mathematical statistics method was used to evaluate the achievement level of students for each criterion. Thereby, the experimental results showed that applying the RME approach in teaching statistical content positively impacted the development of some skills that students needed to achieve. Also, a number of guidelines were provided to guide the enhancement of RME activities.

Keywords:Problem, Realistic mathematics education (RME), Statistics, Grade 7, Mathematical skills, Teaching process.

Contribution of this paper to the literature: This study contributes to existing literature by assessing the effect of a teaching process based on the RME approach on the statistical learning of 7th-grade students and their mathematical skills.

1. Introduction

A proven fact is undeniable in the progress of humanity's long history is that mathematics has a significant impact on the growth of humanity. Not only is it the driving force for science and technology, but math is also a useful tool that is applied in many other fields, from economics, engineering, art education. More than that, math learning facilitates human higher thinking development (Laurens, Batlolona, Batlolona, & Leasa, 2017). Through learning mathematics, students are formed and developed their thinking abilities such as logical thinking, analyzing, synthesis, critical thinking, and creative thinking. Correspondingly, mathematics is required in nearly every level of education and holds a vital position in almost every country's curriculum. With such importance, mathematics education aims to make students interested in learning and learning math and applying mathematics to solve real-life problems. According to Indriani and Julie (2017), mathematics learning will be more meaningful for students if the mathematical ideas are linked to real-life situations. The fact that students understand the intimate relationship between mathematics and practice will become the motivation for students to learn about mathematics, and at the same time, is the basis for students to relate and apply mathematics in fields in practice. On the contrary, if students learn mathematics without being attached to practical experiences, they will quickly forget knowledge and not apply mathematics to other sciences or real-life (Freudenthal, cited by Indriani and Julie (2017)). At that time, the issue has been of correlation between mathematics and the real world has been a problem. For this reason, the theory of Realistic Mathematics Education (RME) was born from the idea of ​​linking mathematics with practice (Uzel & Uyangor, 2006).

The RME is a separate teaching theory of mathematics education, conceived and developed in Finland (Van Den Heuvel-Panhuizen, 2003; Van den Heuvel-Panhuizen & Drijvers, 2014). Developed on the ideas of Freudenthal et al at Freudenthal Institute (Van den Heuvel-Panhuizen, 2000) the theory of RME considers mathematics as a human activity (Freudenthal, led by Van den Heuvel-Panhuizen (2000)). According to Freudenthal, mathematics must be associated with the practice, close to students, and meaningful to society in order for mathematics to have human value. Correspondingly, the practical contexts are one of the defining characteristics of this approach to mathematics education (cited by Van Den Heuvel-Panhuizen (2003)). According to the RME theory, students should learn mathematics by developing and applying mathematical concepts and tools in situations in life (Van Den Heuvel-Panhuizen, 2003).

Furthermore, the RME theory states that instruction must begin with situations and experience, which is demonstrated to be sound and equitable. According to Van den Heuvel-Panhuizen and Drijvers (2014), real-life situations in RME are not only real-life situations but also situations that students can imagine. The extent to which the RME stresses incorporating real experiences into students' perceptions. These situations serve as sources for forming mathematical concepts, tools, processes, and contexts for students to apply mathematical knowledge in the later stages. Simultaneously, students' knowledge will broaden as they master the particular and more general aspects of the topic, thus removing some contexts.

According to Freudenthal (1973) and Gravemeijer (1997), the RME theory has three core heuristics in teaching process design: didactic phenomenon guided reconstruction and self-development model (cited from Sumirattana, Makanong, and Thipkong (2017); Deniz and Kabael (2017); Wahyudi, Joharman, and Ngatman (2017); Uzel and Uyangor (2006); Gravemeijer and Doorman (1999); Yilmaz (2020)). The didactic phenomenon forms the foundation for designing the teaching process in which students explore mathematics by expressing the relationships between a concept and concepts, methods, and other knowledge (Deniz & Kabael, 2017). The second principle - guided reconstruction - reflects the teaching process that gives students the opportunity to self-explore concepts and performs mathematically from real-world problems. Accordingly, math history can be seen as an inspiration to enable students to experience the same process as when that mathematical concept was conceived (Gravemeijer (1997); cited from Sumirattana et al. (2017)). It is important to visualize a possible teaching process so that students can reconstruct concepts (Gravemeijer and Doorman (1999); cited from Deniz and Kabael (2017)). Besides, according to Andriani and Fauzan (2019), self-developed models play a crucial role in bridging the gap and creating a relationship between common knowledge and formal knowledge. Accordingly, students need to be facilitated to develop models themselves and use them in problem-solving (cited by Deniz and Kabael (2017)). Students' initial strategy is typically determined by chance and can be any strategy they wish they have learned before. This model becomes complete through generalization and formalization and can be used as a mathematical reasoning model (Gravemeijer, 1994; cited from Sumirattana et al. (2017)).

One of the basic concepts of Realistic Mathematics Education (RME), according to Freudenthal (1973), is that mathematics is a human activity. As a result, the activity of problem-solving and finding problems, or more generally, organizing the problem from the practical problem or the math problem, is called "mathematics" (cited by Van Den Heuvel-Panhuizen (2003). Thus, mathematics should be taught as "mathematization" (Gravemeijer. & Terwel, 2000). According to Treffers (1993), there are two types of mathematics in mathematics education: horizontal and vertical mathematization (cited by Van den Heuvel-Panhuizen (2000)). In horizontal mathematization, students manipulate mathematical tools to organize and resolve given problems in a practical context (Van den Heuvel-Panhuizen, 2000). The following activities are typical examples of horizontal mathematization: define or describe specific mathematics in the context of a schematic generalization, construct and visualize a problem in many ways, explore relationship, rule, realizing corresponding aspects in different problems, transforming a practical problem into a mathematical problem and converting a practical problem into a known mathematical problem (Uzel & Uyangor, 2006). Meanwhile, vertical mathematization brings about significant improvements to the system, such as providing rules and demonstrating relations (Van den Heuvel-Panhuizen., 2000), for example, presenting formulas, assembling models, and redesigning formulas (Uzel & Uyangor, 2006). Thus, horizontal mathematization goes from practice to signifier, while vertical mathematization involves relations between signs (Van den Heuvel-Panhuizen, 2000). Gravemeijer (1997) describes these two mathematization processes in diagrams, as shown in Figure 1.

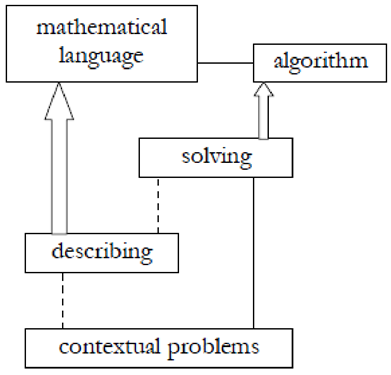
Figure-1. Horizontalmathematization (---); Vertical mathematization (ð)

Source: Aggraini and Fuzan (2018), p.208.

According to Gravemeijer (1997), the RME approach has five principal characteristics. First, it contains a practical context. For some life phenomena, the RME stresses the critical importance of being discovered. Nonetheless, as students' broadened understanding can benefit from these experiences, students will expand their mathematics concepts. Second, it uses models while developing from common knowledge to formal mathematics concepts is a gradual process. Indeed, this process takes place with the help of models and symbols. The use of models is a bridge for students to create their models from practical situations to abstract, or in other words, from general situations to form. Third, the student's contribution is necessary; in particular, students actively build mathematical knowledge based on the foundations and the learning environment that teachers provide, actively solving problems in their way. Fourth, the activity is interactive; for instance, student-teacher interaction, student-student interaction, and student-learning tools are essential in practical math education. As a result, interactive learning activities allow for communication, negotiation, explanation, questioning, question answer, and reflection to form formal knowledge. Fifth, the relationship between the topics is established when mathematical knowledge is related to many other mathematical topics in an integrated form. Mathematical structures and concepts are interrelated; often, it is necessary to explore the relationships of a topic in order for learning to be meaningful (cited by Wahyudi et al. (2017); Indriani and Julie (2017); Luthfi and Suparman (2019); Laurens et al. (2017); Mulbar and Zaki (2018).

The theory of RME sets out many principles for the mathematical teaching process because of the above characteristics. In particular, according to Treffers (1993), there are six core principles in teaching mathematics oriented to the application of the RME theory, including operating principles, practical principles, level principles, principles of interleaving, interaction principles, and guiding principles (cited from Van den Heuvel-Panhuizen. (2000); Van den Heuvel-Panhuizen and Drijvers (2014)).

On the other hand, many recent studies have shown the importance of RME in mathematics education. Since this is the case, it is also necessary for students to develop their mathematical competencies; applied mathematics has a strong connection with practical applications. According to Yuanita, Zulnaidi, and Zakaria (2018), the approach to RME allows students to create knowledge from the topics they have already learned. Also, students can communicate their ideas as long as they can firstly, they will be able to communicate the concepts that go with each learning stage. It is through this process that students have confidence in producing learning outcomes on their own. Furthermore, the study of Yuanita et al. (2018) confirmed that RME is one of the most effective teaching approaches to fostering competencies in mathematical representation and problem-solving (Drijvers, Kodde-Buitenhuis, & Doorman, 2019; Laurens et al., 2017; Yuanita et al., 2018) and student math trust. Besides, the RME creates favorable conditions to develop mathematical reasoning and mathematical communication competencies (Aggraini & Fuzan, 2018; Andriani & Fauzan, 2019; Habsah, 2017; Laurens et al., 2017; Supriyanto & Hairun, 2020; Widada, Herawaty, Yanti, & Izzawati, 2018; Yerizon & Ismail, 2020) . More importantly, applying practical math education in teaching also contributes to developing students' thinking ability (Drijvers et al., 2019; Laurens et al., 2017), especially critical thinking (Palinussa, 2013).

The RME theory can dramatically expand on the range of functions that teachers can perform in their respective fields and the types of resources they have at their disposal and applying RME, textbooks, and tools need for these jobs is extremely important. On the role of teachers, the author (Sumirattana et al., 2017) argued that teachers play an essential role in improving students' mathematical abilities to apply mathematics in practice further, and this is the result of teaching methods that teachers apply. In realistic math education, the teacher acts as a facilitator, providing the basis for practical interpretation and connecting the math curriculum with practice (Aggraini & Fuzan, 2018; Habsah, 2017) is assessors while students think, exchange ideas, train students to be democratic by respecting the opinions of others (Hasibuan & Amry, 2017). In a supportive learning setting, teachers create an environment that students can succeed (Wahyudi et al., 2017). The textbook's applied math education concepts also serve as tools for a higher-level understanding of theory. According to Djokic (2014), the appropriate structure of lesson units according to the teaching approach based on "practical context" can help achieve a positive effect on students' potential in learning concepts and mathematical processes and problem-solving. Recognizing the significance of RME for math education as well as the role of textbooks for the practical math education-oriented teaching implementation, many studies have proposed the renewal of mathematics curriculum and textbooks due to certain limitations of the current program to the application of the practical approach in mathematics education (Djokic, 2014; Luthfi & Suparman, 2019; Trung, Thao, & Trung, 2019) . Additionally, the learning cards and other tools, such as word lists, play a critical role in enhancing practical mathematics's teaching effectiveness. Nevertheless, according to the RME approach, the student's learning card has the following characteristics: practical contexts, construction, mathematical models, interaction, and cumulative learning (Basuki and Wijaya, 2018; cited from Supriyanto and Hairun (2020)).

Nonetheless, both teachers and students have considerable difficulties applying mathematical methods and learning strategies in their respective fields. Research by Meika, Suryadi, and Darhim (2018) has shown that when learning practical math, students often have difficulty in simplifying the problem, forming a mathematical model (horizontal mathematization), completing a mathematical model (vertical mathematization) as well as in interpretation and verification. Besides, students' ability to apply mathematics in solving practical problems is also limited. Accordingly, students have difficulty adapting to the types of problems given and organizational methods of practical learning activities. Also, students are not active in exploiting important information of the problem; in general, students' skills in reading and understanding problems are still limited; a given context has not been fully exploited and examined deeply; the student's modeling capacity is still limited (Trung et al., 2019).

Furthermore, teachers and trainees are faced with numerous difficulties when they are tasked with incorporating the RME into their lessons. Research by Wahyudi et al. (2017) pointed out that the trainee teacher encountered the following obstacles: (1) the teacher did not have a deep understanding of math teaching knowledge, (2) the teacher was not familiar with the problem. Regarding practice in math learning, (3) teachers are not familiar with using visual teaching/communication tools in mathematics, (4) teachers know many methods of maths teaching techniques but typically do not employ all of them, (5) teachers have not yet received the training they need to adequately meet the lesson preparation requirements, (6) teachers do not have the necessary simulation skills in order to provide excellent instruction in mathematics.

Accordingly, in order to overcome obstacles for trainee teachers in teaching practical mathematics, the study of Wahyudi et al. (2017) proposed the following solutions: (1) reinforcing the mastery of teaching knowledge and mathematical concepts, (2) strengthening the relationship between teaching knowledge with practical problems. (3) fortifying the ability to identify and use visual / communication tools in math teaching, (4) reinforcing a variety of teaching methods, (5) consolidating standardized ability to have teaching lesson plans, and (6) strengthening the ability to simulate.

Realistic Mathematics Education (RME) for many years has been an interest of many researchers. In terms of theory, many studies have inherited and developed Freudenthal's views on RME, such as Van den Heuvel-Panhuizen (2000); Van Den Heuvel-Panhuizen (2003); Van den Heuvel-Panhuizen and Drijvers (2014); Gravemeijer and Terwel (2000). Studies have shown the formation and development of RME, basic concepts, characteristics, and core principles in teaching design following the math approach, practical learning. Based on the spirit of enriching mathematics learning, the authors, Lizzeth and Omar (2021), have used virtual practices to aid university students' learning.

Furthermore, many studies have shown a close relationship between the RME and the development of different types of math competencies of students (Aggraini & Fuzan, 2018; Drijvers et al., 2019; Habsah, 2017; Laurens et al., 2017; Luthfi & Suparman, 2019; Palinussa, 2013; Sumirattana et al., 2017; Trisnawati, Pratiwib, & Waziana, 2018; Uzel & Uyangor, 2006; Widada et al., 2018; Yerizon & Ismail, 2020; Yuanita et al., 2018) . Research by Laurens et al. (2017) was performed to clarify the differences in students' mathematical perception when applying RME compared to conventional learning. The empirical impact includes math learning following an RME approach and traditional learning. The study results through the t-test showed the difference in mathematical perception of the experimental group and the control group. As a result, students were taught according to the RME approach outperform those who study using the traditional method. Research emphasizes the importance of developing students' thinking abilities through RME and games to create meaningful and practical learning environments. Besides, Palinussa (2013) conducted a study with pre-experimental and post-experimental surveys on the experimental group to assess the capacity of mathematical critical thinking and personality through RME. The tools used in the research include exams of math skills, surveys of critical thinking ability, and cognitive scales of students. Data were analyzed by the t-test method and ANOVA method. Accordingly, the study shows that the results and improvements in critical thinking and the students' quality are better influenced by realistic math education than students learning by traditional methods. A study by Trisnawati et al. (2018) to obtain a description of the application of RME can improve students' mathematical communication ability. The type of research used is classroom action research, which deals with Kemmis and Mc's design. Taggart's research including planning, action, observation, and reflection. According to the RME approach, the research results show that applying mathematics teaching can improve students' mathematical communication ability. Hence, the learning process of mathematics is carried out in accordance with RME characteristics such as using practical context (teachers present practical problems and ask students to learn the given problem), using models (students model using tools to address problems), using student achievement and constructivism (teachers provide opportunities for students to solve problems and let students communicating answers), interaction (teacher-student interaction and student-student interaction), and integration (combining a unit with other lessons with other scientific fields).

All reduction that first emerged in mathematics had several new studies to raise the subject's quality since then led to an increase in research in RME studies. The research of Deniz and Kabael (2017) analyzes the concept of the student's angle coefficient when the teaching process is designed involved with the theory of RME has shown in the process of students re-forming the concept of angle coefficients through developing right triangle model. Accordingly, the development of the model takes place in three phases: (1) the interpretation tool is context-dependent, (2) the tool used to compute the angular coefficient, (3) the cognitive tool. In particular, Andriani and Fauzan (2019) show the positive effect of designing and teaching statistical concepts following RME to develop students' mathematical communication skills. Additionally, the positive impact of the approach to realistic mathematics education is also studied through the application in teaching contents such as the cosine theorem (Loc & Tien, 2020) the first-degree functions in one unknown (Loc & Hao, 2016) functions (Makonye, 2014) and logarithms (Webb, Van der Kooij, & Geist, 2011).

Moreover, teacher training and retraining's effectiveness also directly affect applying the RME in mathematics education. Research by Wahyudi et al. (2017) with research focuses on the theoretical development of RME, improving the effectiveness of math education with RME, difficulties, and solutions in applying RME to practice teachers the primary schools. Research has identified (1) five steps to apply RME to trainee teachers, including case/problem exploration, explanation of practical problems, solving practical problems, comparing, and discussing options, make conclusions; (2) the application of RME can enhance teaching effectiveness in mathematics; and (3) the difficulties of the trainee in applying the RME include: teachers do not have a deep understanding of math teaching knowledge, teachers are not familiar with issues related to practice in math learning, the teacher is not familiar with using visual / communication teaching tools in mathematics, the teacher has not mastered many math teaching methods, the teacher has not yet met the teaching preparation skills, judgment, teachers do not have enough simulation skills in teaching math. Since then, the research has proposed corresponding solutions to overcome the above difficulties. Besides, Yilmaz (2020) has researched teachers' perception of RME. Hence, the study analyzed the results of answering open questions about RME of 32 trainees after learning about teaching approaches, including RME. According to our research, trainee teacher surveys, most teachers believe they are equipped with theoretical knowledge of RME. However, the ability to distinguish RME similarities and differences from other teaching approaches and the ability to set real-world problems following the RME orientation is still limited.

Statistics is the subject of learning about organizing, collecting, analyzing, interpreting, and representing data. Not only has significance in mathematics, but statistics can also be used in all fields of science, including natural sciences, social sciences, business, economics, and industry (Koparan, 2015). Mullis, Martin, Ruddock, O'Sullivan, and Preuschof (2011) have given the required requirements for statistical content as follows: students can arrange simple data sets or have been able to work with the data already collected; students can understand data, symbols, and key points in data presentation. For example, students can identify numbers representing statistical values ​​and numbers that represent the frequency of occurrence. Nonetheless, their investigation of Andriani and Fauzan (2019) indicates that students' difficulty in learning statistics is magnified in classes. Among these difficulties, students may have obstacles in distinguishing the meaning of the concepts of mean, fashion, and median, especially when applying formulas—differences in problem-solving (Nugroho, 2013; cited from Andriani and Fauzan (2019)). Furthermore, research has also shown that one of the factors that affect students' statistical learning difficulty is that the process of teaching and learning mathematics is not linked to practice (Andriani & Fauzan, 2019). Because of this is how critical, according to Gil and Ben-Zvi (2011), statistics is for students to know and understand is how to contextualize it is.

2. Theoretical Framework

2.1. Orientation for Teaching Organization

Based on the teaching process applying the RME approach in math teaching, teaching situations are organized for students to study in the classroom, as shown in Figure 2.

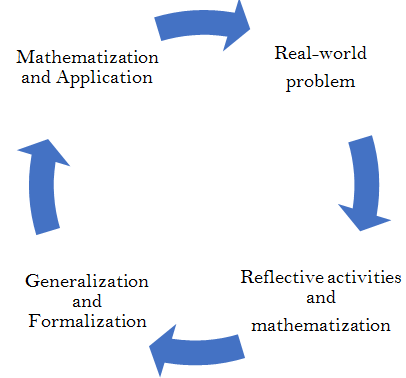
Figure-2. Mathematical process using RME theory

Accordingly, the teaching process-oriented to apply RME theory is organized in five steps as follows:
Step 1: Organize for students to learn practical situations.
Step 2: Explain the problem in context.
Step 3: Solve the problem according to the context.
Step 4: Compare and discuss the answers. Conclude.
Step 5: Teacher lets students practice applying the knowledge they have learned.

2.2. Statistics in Math Curriculum and Textbook of Vietnam

The content of statistics is presented in Chapter III, Algebra section, textbook 7 volume 2 (Chinh et al., 2015). The objectives of this chapter have the following ideas:

1. Initially, understand some basic concepts such as initial statistics table, sign, sign value, frequency, "frequency" table (experimental distribution table); the formula calculates the mean and its representative significance, meaning the fad the role of statistics in practice.
2.  Know how to collect data from small, simple surveys close in learning in life (knowing how to tabulate from baseline data collection to "frequency" form.
3.  Know how to find different values ​​in the statistics table and frequency respectively, tabulate "frequency". Knowing the chart representation of the above column. Knowing the chart is aware of the distribution of the signal's values ​​through the "frequency" table and the chart.
4.  Know how to calculate the average number of signs according to the formula and know how to find the trend of signs.
The textbook's statistical content is presented in four lessons and revision and is summarized systematically in the order of knowledge and skills that need to be achieved, as shown in Table 1.

Table-1 . The contents of statistics in grade 7.

Lesson Knowledge Skills
Collect statistics, frequency Signal
The value of the sign frequency		 Identify signs
Prepare baseline datasheet
Find different values in a range of values
Find the frequency of each value
Table "frequency" Structure frequency board
The convenience of the frequency table compared to the original datasheet		 Table the frequency
Comment from the table "frequency"
Chart Meaning of the chart: Gives a visual representation of the signal Draw line graphs, bar charts
Comment on the chart
The average number, the fashion of the sign The formula for calculation average
The meaning of average
The meaning of the fad of the sign		 Calculate average by the formula from the table.
Find one of the signs

Source: Chinh et al. (2015).

This text will expand on the scope of mathematics by providing a sampling of comments and a collection of analysis and statistics. Regardless of the book they use, students can provide some basic concepts to expand their knowledge of descriptive statistics. Indeed, the textbooks focus on training students' practical skills to grasp basic concepts, some ways of presenting data and familiarize themselves with formulas for calculating some characteristic parameters. A limited resource for those needing simple concepts and formulas in textbooks is mainly used to reinforce the simple ideas and formulas from theory in the section.

For data presentation, in addition to forming the skills of making "frequency" and "charting" tables for students, the textbook also enhances the types of math comments on frequency tables and charts to help students. It is part of students' education to compare a value against a value in a value range. Nonetheless, the mathematical patterns involved in comparing two or more different numbers of the same sign are not mentioned.

Surveys were conducted on all aggregate units, but the common feature was that they were in a narrow range (mostly below 30 values) and associated with simple numerical signs. In it, the students were not used to sampling to make the survey useful. Questions and statistics overlap, apply, with people asking which cases or situations most likely represent specific realities and what they know and applying their statistics to those used to learn. It has yet been challenging to develop initiative and creativity in situations leading up to this point, such as concept discovery and definition and theorem proofs, since these have not stimulated that before having teacher inactivity.

Vietnamese textbooks have given some real-world problems to train students' problem-solving abilities. Nevertheless, most of the problems are built-in types of math, do not highlight the significance or application of statistics in practice. Students will be unable to discern how similar the problem results are to the actual situation because they cannot see all of the problems at the same time this information is provided. To help their students prepare for all possible future circumstances, teachers should construct real-world problems their students can work on, then test students' capacities to understand them.

Furthermore, the proposed activities have not clearly shown the ability to apply knowledge to resolve practical situations. The practice of solving real-world problems is more simulating and very close to the mathematical model, that is, only interested in calculating, answering the question stating the task to deal with the problem, paying attention to the step from empirical data to a mathematical model to handle. Training students in problem-solving means ensuring that teachers understand and appreciate the role of statistics requires attention and compassion. Also, teachers should include many practical situations when covering each topic in lessons so students can be ready to deal with many of their own to allow students to become proficient at dealing with actual scenarios.

2.3. Orientation to Organize the Assessment

In keeping with the textbook information contents in grade 7, the following skills are required for these materials in Table 2.

2.4. Research Purposes and Questions

This study has the purpose of determining the effectiveness of a teaching process based on the RME approach to the statistical learning of 7th-grade students. Besides, the present study aims at identifying the effect of a teaching process based on the RME approach on students' mathematical skills. The two research questions posed are associated with the above research objectives.

  1. To what extent does implementing a teaching process based on the RME approach contribute to students' learning of statistics at the junior school level?
  2. What effect does a teaching process based on the RME approach have on students' mathematical skills?

Table-2 . Required skills for the content of statistics in grade 7.

Skill Criterion Levels
Level 1 Level 2 Level 3 Level 4
Collect and organize data (Skill 1) Collect, classify and represent data according to given criteria (criterion 1) cannot explain the collection and classification of data according to given criteria. Implement and justify the collection and classification of data according to the given criteria. Explain the reasonableness of the data according to simple mathematical criteria. (example: rationality, representativeness). -
Describe and represent data on tables and charts (criterion 2) Can not read and describe the data in the form
statistical chart.		 Proficient reading and description of data in the form of statistical charts. Select and represent data in an appropriate table and chart. Recognize different representations for a data set.
Analyze and process data (Skill 2) Forming and solving simple problems arising from existing statistical figures and charts (criterion 3) Not realizing the problem or simple law. Identify problems or simple rules based on the analysis of the data obtained. Solve simple problems related to the data obtained. -

3. Methodology

3.1. Participants

The study conducted experiments on 48 students of class 7A6 at Tang Nhon Phu B Junior School, District 9, Ho Chi Minh City, Vietnam. The experiment was organized to verify the RME approach's effectiveness in teaching statistical content through the intrinsic validation method. To ensure the quality of the teaching practice, we included participants who were both able and willing to help. The study also discovered that students' prejudice and lack of respect were not a part of the experiment, indicating that the students were neither negatively impacted nor benefited from the absence of these characteristics.

3.2. Research Design

The process of pedagogical impact on the experimental class after students take the pre-test (Problem 1) is summarized in the following diagram Figure 3.

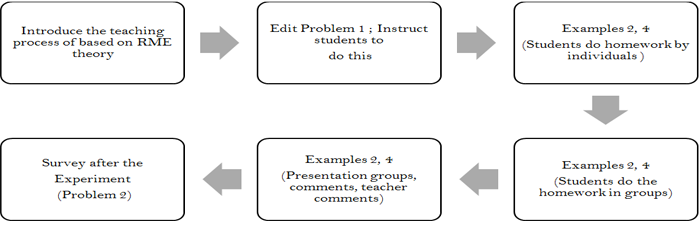
Figure-3. Diagram showing the experimental progress.

The experimental process was carried out through 3 phases as follows.

Phase 1. Students work through the requests on the worksheets prepared by teachers in a personal format within 15 minutes.
The objective of Phase 1: Create opportunities for students to express their abilities, think and solve situations independently. Thereby, students show their ability to cope with practical situations by building relationships between different factors already in the situation, transferring real-world problems to math problems, solving math problems to cope with the situation, and considering the reasonableness of dealing with the situation.Phase 2. Students work through the practical situations they did in phase 1 in a group format (a group of 11 students or 12 students) in 10 minutes.
The objective of Phase 2: Create conditions for students to review their work and comment on their work in the group. Thereby, students discuss and present ideas to protect their personal views or contribute to their work and collect their friends' opinions to complete the group's work together.
Phase 3. Validation - the class is still working in groups and correcting with the teacher. Each group nominated a representative student to present their homework, other groups to comment and contribute. Groups can then argue for better results. Then, the teacher comments on each group's work and guides the groups' problems to improve each group's work. Processing time: 20 minutes.

The objective of Phase 3: Students will consider the group exercises in phase 2 in phase 3 with limited intervention from the teacher. This is the phase where generalizing and formalizing knowledge helps students step by step improve real-world problem-solving skills.
The scenarios used in the experiment are designed as follows.
a) Problem 1 - Survey situation before the experiment
Problem 1. The goals scored in the last ten matches by soccer players A and B are recorded in Table 3:

Table-3 . Results scored by players A and B.

Football player A
0
1
1
1
3
1
2
1
1
1
Football player B
0
0
5
0
0
4
3
0
0
1

If you were your team's head coach, which player would you choose to be on your team? Explain why?

Situation analysis: The scenario provides a table of goals for two players and asks students to pick a player on their team based on the board. There are a simple cause and clear understanding of the problem requirements, so students can easily visualize the problems presented with this circumstance. However, students may have difficulty converting real-world problems to math problems. This may be because students have obstacles in applying the problem's results to give an appropriate answer to the situation. After all, students do not understand the meaning of the real-world problem. Mathematically, the given assumptions are related to the averaging of goals scored per game. Hence, students may consider summing or averaging to resolve problems.

b) Example 2, 4 - Teaching situation

In the process of organizing the experiment, through observing students' expressions, learning about their knowledge and experience, the research team made necessary adjustments, step by step, completing the situations. The scenarios used in three experimental phases are designed as follows:

Example 2. a) Shooter player A's scores are given in Table 4. Calculate the average score of athlete A.

Table-4. Results scored by player A

Scores
7
8
9
10
Number of shots
2
3
10
5

b) The score of shooter B is shown in Table 5. Predict which athletes are performing better. Why?

Table-5 . Results scored by player B.

Scores
7
8
9
10
Number of shots
2
3
10
5

Situation analysis: The purpose of Example 2 is to assist students to realize that in solving the problem, it is necessary to use the mean (in question b) and allow the students to see the representativeness of the mean when comparing the average number. Compare signs of the same type.

Example 4. The number of water bottles a student in class 7A1 drinks every day is in Table 6.

Table-6 . The number of water bottles drunk by a student in class 7A1.

0
1
5
4
3
2
4
0
0
1
2
3
4
1
0
0
2
3
4
2

Calculate the average from the table above. Do you think the average is appropriate to say how many bottles of water you drink every day? Why and why not?

Situation analysis: This activity supports students in practicing speaking into words, analyzing, reading information from the datasheet, and drawing comments from the datasheet. Also, it shows students that in some cases, the average cannot represent a sign.

c) Problem 2: Post-test

Problem 2. Your family plans to organize a weekend trip, but your mother does not like it raining. You went online to search for information about this week's rainfall in 2 locations (given in Table 7) that your family chose and got the following results:

Table-7 . Statistics of rainfall in a week in Vung Tau and Phan Thiet.

 
Monday
Tuesday
Wednesday
Thursday
Friday
Saturday
Sunday
Vung Tau
0.1 mm
4.2 mm
5.2 mm
3.8 mm
18.4 mm
19.6 mm
20.6 mm
Phan Thiet
0 mm
2.9 mm
8.8 mm
22.1 mm
22.7 mm
10.8 mm
11.2 mm

a) Help your mother to choose a suitable tourist destination. Explain why?
b) Do you choose a location with lower average rainfall? Why?
Situation analysis: Situation refers to selecting the right venue for the conditions where no rain occurs on the weekends. Students rely on their knowledge of the mean to compare the average rainfall in the two locations and comment about the rainfall situation. Then, to make the right choice, learners need to incorporate the requirements "mom does not like rain" and "organizes a weekend tour."

3.3. Data Collection and Analysis

Data was collected through the results of a pre-test, study report, and post-test. Additionally, students' learning manifestations and attitudes were also observed and analyzed qualitatively. The mathematical statistics method was then used to evaluate the skill criteria' achievement level in the lesson "statistics" of students in the experimental class. Simultaneously, the experimental process results would show the effectiveness of applying RME in teaching this content. Moreover, frequency statistics and the student population's percentage value were taken to measure their mathematical skills' achievement level. Another highlight was the detailed analysis of some students' exercises to evaluate students' skills. Since then, some of their difficulties and errors were also pointed out. To have the convenience of analyzing the above data, the students were coded from Student01 to Student48.

4. Results

4.1. Pre-test Results

Based on assessing the degree of achievement of the required skills criteria outlined in Table 2, the pre-experimental survey results (Problem 1) were listed in the following table.

Table-8. Statistics of pre-test results.

Levels
Criterion 1
Criterion 3
Frequency
%
Frequency
%
1
-
-
33
68.1
2
-
-
11
22.9
3
2
4.2
4
8.3

The statistical results in Table 8 showed that most students did not address the simple problems from the data already in the situation (criterion 3). The percentage of students who were assessed at level 1 was 68.1%. Students did not resolve problems arising from given data, maybe because they had few opportunities to apply mathematics in real-world situations. A small number of students recognized the problem by analyzing the data (22.9%); only four students (8.3%) could cope with the problem related to the data collected. In the criteria of collecting, classifying, and representing data according to the given criteria (criterion 1), only two students (accounting for 4.2%) could explain the reasonableness of the data according to the criteria math problem (to represent the mean number). While most of the students were under the impression that it meant the minority (46 students) was unrepresentative, most were incorrect. The student24 made the following mistake.

Problem 1. The goals scored in the last ten matches by soccer players A and B are recorded in Table 9:

Table-9. Results scored by players A and B.

Football player A
0
1
1
1
3
1
2
1
1
1
Football player B
0
0
5
0
0
4
3
0
0
1

Answer
I choose player B because there are many games he has scored more goals, his number of goals is more than player A.

4.2. Results Related to Three Phases of Teaching

4.2.1. Study Report Results: Example 2

Students’ work in the study sheets in each phase was also evaluated based on the criteria in Table 10 to show the student's skills progress in learning statistical content in the direction of logical application of the RME.

  1. Phase 1.

Table-10. Statistics on the student's exam results in Example 2 - Phase 1.

Levels
Criterion 1
Criterion 3
Frequency
%
Frequency
%
1
-
-
-
-
2
20
41.7
23
47.9
3
28
58.3
25
52.1

In criterion 3, 47.9% of students solved the problem by using the average number. In criterion 1, 58.3% of students recognized that the average number should be used as a representative for comparison. The considerable increase in the percentage of students who were assessed at level 3 was because they had recognized the mean's representativeness to make the comparison. The typical student related to this was Student19.

Example 2. a) Shooter player A's scores are given in Table 11. Calculate the average score of athlete A.

Table-11 . Results scored by player A.

Scores
7
8
9
10
Number of shots
2
3
10
5

Answer: The average score of athlete A: 8.9

  1. The score of shooter B is shown in Table 12. Predict which athletes are performing better. Why?

Table-12. Results scored by player B.

Scores
7
8
9
10
Number of shots
2
3
10
5

Answer: The average score of athlete B: 9.1
Conclusion: Player B does better because athlete B has a higher GPA.

Besides, a common mistake was that even though students had calculated the average, they did not use the results to compare two athletes (with 20 students). The students' assignments' errors were due to the confusion between the number of shots and average scores in the performance assessment. The following was a typical exercise. Student17's worksheet was an example of another common mistake among most students (23 students). As a result, they drew conclusions based on not showing their data, even though the comparison or calculation was lacking. The statistics showed that in criterion 1 and 3, level 3 increased compared to the surveyed situation, specifically reaching 58.3% for criterion 1 and 52.1% for criterion 3. The students' overall results with regard to the surveys were better than their results when doing similar tasks. However, over 40% of students needed more practice to understand the average's representativeness in applying practical problem-solving.

b) Phase 2
The results of Example 2 students working in groups were shown in the following table.

Table-13. Statistics on the test results in Example 2 of groups - Phase 2.

Levels
Criterion 1
Criterion 3
Frequency
%
Frequency
%
1
-
-
-
-
2
1
16.7
0
0
3
5
83.3
6
100

It was evident from the results in Table 13 showed that in phase 2, after discussion and adjustment, the groups achieved relatively good results. Nevertheless, Group 2, although calculating the average, still used the term "total score" to compare two athletes. It was noteworthy that the proportion of groups rated at level 3 for both criteria was above 80%.

c) Phase 3

By observing the group discussion in Phase 3, the phase results were recorded as follows. Groups argued about whether to use the average or the total score to make predictions about the campaign tablets' performance. After Group 2 completed their presentation, the other groups contributed their ideas, and Group 2 conducted their criticism. The reasoning of Group 3 was convincing, so the members of Group 2 recorded their opinions and learned from experiences. This expression was one possibility, but the solution to the original problem was the answer that arrived at by computation. For this reason, the situation was quite clear; students only needed to answer the question to expand on the subject and only argue the conclusion about the question itself.

4.2.2. Study Report results: Example 4

1. Phase 1

The results of the student work in Example 4 were listed in Table 14.

Table-14. Statistics on the student's exam results in Example 4 - Phase 1.

Levels
Criterion 1
Criterion 3
Frequency
%
Frequency
%
1
-
-
-
-
2
29
60.4
31
64.6
3
19
39.6
17
35.4

Table 14 showed that although students had calculated the average to provide an explanation, the percentage of students who only reached the level of problem recognition on data analysis (level 2) was quite an excellent high, reaching 60.4%. This may be due to the student misunderstanding the unit of measure (water bottle instead of a liter of water), leading to misinterpretation. Thus, the percentage of students who perceived the mean increases' representativeness increased compared to Example 2 (reaching 64.6%). Nevertheless, this was not the expected outcome of this situation. Moreover, the remarkable results were that there were still students who calculated the arithmetic mean and realized that the mean's representativeness was inconsistent. Despite their attempts, however, they were unable to provide a reasonable explanation. Here was a typical worksheet of Phase 1.

Example 4. The number of water bottles a student in class 7A1 drinks every day is in Table 15.

Table-15 . The number of water bottles drunk by a student in class 7A1.

0
1
5
4
3
2
4
0
0
1
2
3
4
1
0
0
2
3
4
2

Calculate the average from the table above. Do you think the average is appropriate to say how many bottles of water you drink every day? Why and why not?

Answer

(1+5+4+3+2+41+2+3+4+1+2+3+4+2) : 20 =2.05

In my opinion, not because of the daily water he drinks too little, and the person who drinks at most is 3 liters of water a day.   

2. Phase 2

The results of the assignments of the groups in Example 4 were listed in Table 16.

The analysis revealed that all the groups had fixed the problems attributed to the member assignments and returned a vast improvement in the progress in their work overall. Consequently, there was no group task at level 1 or level 2. Besides, in contrast to the above example, which focused on two small groups of people, this proves that the groups in Example 2 were more effective. Having thus defined their meanings, the groups came to understand the terms and concepts. The effects of this problem led the students examined to indicate that students gained a deeper understanding of the situation. Students remained uninvolved in group activities; however, passively observing and participating in other people's daily group activities allowed them to explore their expanded potential fully.

Table-16. Statistics on the test results in Example 4 of groups - Phase 2.

Levels
Criterion 1
Criterion 3
Frequency
%
Frequency
%
1
-
-
-
-
2
0
0
0
0
3
6
100
6
100

3. Phase 3

Observation results of students' group work in Phase 3 showed that students gave each other ideas to understand the mean's representativeness and answer the situation. During the discussion, some students discovered their mistake in misunderstanding the arithmetic mean's representativeness outlined in Phase 1. Accordingly, after being commented on by friends and teachers, students could understand when it was possible / not possible to use the average as a representative.

4.3. Post-test Results

Based on assessing the degree of achievement of the required skills criteria outlined in Table 2, the post-experimental survey results (Problem 2) were listed in Table 17.

Table-17. Statistics of the results of the survey situations after the experiment.

Levels
Criterion 1
Criterion 3
Frequency
%
Frequency
%
1
-
-
-
-
2
5
10.4
33
68.8
3
43
89.6
15
31.2

According to the statistical results in Table 17, the percentage of students who explained the reasonableness of the data according to the simple mathematical criteria (representing the mean) had increased significantly. Nonetheless, some students were not rated at level 3 because they calculated the average number but did not understand the representativeness of the average in problem-solving applications (68.8%). Additionally, the answer to the situation's questions showed that students had achieved good stability in their analytical ability and understanding the meaning of the problem to give answers to the situation. An expected result was that the percentage of students explaining the reasonableness of the data reached 89.6%, and solving a simple problem related to the obtained data reached 31.2%, much higher than the result of the survey before the experiment.

After experimentally teaching statistical content in the direction of applying RME, through analyzing and comparing survey results before and after the experiment, it was possible to conclude that students in the experimental group made progress on some skills that required the statistical content. Specifically, students met the criteria of two skills (1) collecting and organizing data, (2) analyzing and processing data. Accordingly, the percentage of students achieving the highest level of each criterion had a significant increase after learning under the impact of RME. For data collection and organization skills, the rate of students meeting the criterion "Collect, classify, and represent data according to the given criteria" (criterion 1) was at the highest level" like to have the reasonableness of the data according to simple mathematical criteria (e.g., rationality, representativeness)" reached 89.6%, an increase of 85.4% compared to the rate of students meeting this criterion in the test following experiment (4.2%). For data analysis and processing skills, the rate of students meeting the criterion "Forming and solving simple problems arises from the existing statistical data and charts" (criterion 3) in the best level "Solving simple problems related to the obtained data" reached 31.2%, compared with the rate in the pre-experimental survey result (8.3%) increased to 22.9%.

5. Discussion and Conclusions

Through analyzing the change in student performance through each teaching phase, it can be seen that students have progressed step by step in problem understanding skills, problem-solving methods as well as increasingly master the concepts and their meanings in specific situations, such as the representativeness of the arithmetic mean. Moreover, the results of observing classroom activities show that the teaching phases designed according to the orientation of the RME stimulated the initiative to occupy knowledge, the cooperation in students' learning, mathematical communication, critical thinking skills, as well as enhancing the interaction between teacher-student and student-student subjects in the classroom. Thereby, it shows that students' horizontal mathematic and vertical mathematization takes place in the teaching phases and achieves significant efficiency. The results of the study have similarities with some studies of the authors Sumirattana et al. (2017); Yuanita et al. (2018); Deniz and Kabael (2017); Andriani and Fauzan (2019); Loc and Hao (2016); Loc. and Tien (2020); Uzel and Uyangor (2006); Webb et al. (2011); Laurens et al. (2017); Palinussa (2013); Makonye (2014); Aggraini and Fuzan (2018); Hasibuan and Amry (2017); Trisnawati et al. (2018); Widada et al. (2018). According to research, however, it can be shown that mathematics is challenging for students even after they have the ability to answer complicated questions effectively. One of the reasons given is that students are familiar with traditional learning methods, passively learning and acquiring knowledge as the teacher's central role. This is also the judgment of the studies Aggraini and Fuzan (2018); Habsah (2017); Laurens et al. (2017); Makonye (2014); Mulbar and Zaki (2018).

For this reason, to promote the useful application of RME, learning content and teaching methods need to be improved. Additionally, teachers' roles will need to adapt to meet new situations, so the student population's status must be expanded to encompass their roles. The learning program is necessary to design learning content that is open and associated with the practice, stimulating students' active learning and self-thinking. If a proper teaching and learning program is formulated, it will give teachers opportunities to become better teachers. Moreover, based on ensuring harmony with educational goals, the principles of teaching design according to the RME approach should be placed among the principles of designing talent. learning materials, and mathematics teaching methods. At that time, the student becomes the center of the learning process, and the teacher, from the central role, becomes the instructor, advisor, and evaluator of the student's learning process. Roles and methods have changed, and the need for specialized teaching content and innovations, so teachers must be highly prepared to employ RME in teaching. Specifically, teachers need to equip with solid professional knowledge, understand the educational objectives and perspectives of the subject education program and have a basic grasp of problems related to the theory and application of RME in teaching. Consequently, teachers need to be dynamic, creative, and innovative in lesson design, develop learning tools and means suitable for teaching content and practical contexts. In terms of lectures, teachers need to learn about the history of formation and the nature of mathematical concepts to find practical problems matching the necessary concepts to teach. Besides, teachers need to cultivate the ability to convert a practical problem into a math problem or build a simulated practice problem suitable to the student's level and the learning environment's primary conditions. Furthermore, teachers' and students' roles, learning tools or means, and the learning climate in specific classes are issues teachers need to plan and well-prepared. Simultaneously, teacher training and retraining also play a crucial role in developing practical math education theory in teaching mathematics. On the other hand, educational authorities, as well as schools, need to have a leading role in designing learning programs and teaching methods oriented to practical math education, and at the same time must create favorable conditions benefit in a realistic environment, facilities for teachers, and students to access practical math education effectively and effectively. In terms of research, it is possible to conduct research related to the application of RME in other mathematical contents and the effectiveness of this teaching approach in developing students' math competencies. Also, the research on the influence of RME on students' learning attitude, mathematical beliefs, and interest in learning is worth considering.

Some recommendations are given to guide the enhancement of math teaching activities using the RME approach. In addition to building practical problems derived from existing problems, the teacher needs to design learning activities. Accordingly, in this activity, teachers need to focus on critical concepts' importance, not too intensely focused on general teaching stages or general description. Firstly, a teacher can use problems from the world around them to create problems and discuss and address them. Teachers often perform that task to put the problem on a new lesson or transition from the previous item to the next item in the lesson. When motivated, teachers can bring realities closer to students; vast social reality (economic, technical, defense); reality in other subjects and sciences. Nevertheless, teachers also need to pay attention to the actual problems given that they need to ensure authenticity, do not require too much additional knowledge, the way from the point of issue to the problem of solving the problem is as short as possible. Secondly, teachers use real-world problems to help students expand their understanding. The reinforcement stage is best used to ensure students' understanding of objectives in the teaching process. Also, this is the vital first step in testing teaching and learning processes for educators and pupils, where they can identify if they are making progress. This point is emphasized in this stage; teachers can work on challenging mathematical problems while also being dedicated to ensuring that students gain depth in their knowledge. Teachers should explain to students that they see how vital it is to comprehend real-life situations and that mathematics is in their decision to commit knowledge to memory, allowing them to focus on learning and knowing the answers.  When teachers take their students out of the classroom and into the field, they enhance their mathematical capabilities and teach about practice, allowing students to understand situations more closely to the problems that they will face on the job. As opposed to end-of-the-year examinations, where end-of-chapter problems are used to practice prior knowledge, practice problems are provided in class to study for exams and a few review classes. This way is especially advantageous when practical problems are the integration and connection of knowledge contents. Students apply the knowledge they have learned into practice periods, know the applications of mathematics in practice, and at the same time train competencies such as computational ability, ability to use measuring tools, draw, feature, cooperate, practice measurement skills in practice for students. From this, students understand the true essence of mathematics as a stepping stone to test their understanding of reality. In addition to the practical lessons according to the program distribution, teachers can offer other practical problems integrated into the class (for simple practice problems) or group and assigning tasks to go home. Finally, the teacher gives the test with situations that reflect a practical application. The tests are an essential basis for teachers to evaluate the learning situation, knowledge-building situation, and practice skills regarding students' abilities, attitudes, and qualities. Thereby helping teachers adjust the teaching process later; students are also aware of how far they have grasped the gaps or errors that need efforts to overcome. Today's exams and tests consist of information stored in memories but little in applying it to real-world situations. In the tests, teachers should place practical examples and experiences close to their students' situations. This will benefit students by equipping them with the skill of using real-life examples.

Citation| Bui Phuong Uyen; Duong Huu Tong; Nguyen Phu Loc; Le Nguyen Phuoc Thanh (2021). The Effectiveness of Applying Realistic Mathematics Education Approach in Teaching Statistics in Grade 7 to Students' Mathematical Skills. Journal of Education and e-Learning Research, 8(2): 185-197.
History: Received:10 February 2021/ Revised: 12 March 2021 / Accepted:8 April 2021/ Published:27 April 2021  
Acknowledgement: All authors contributed to the conception and design of the study.
Funding: This study received no specific financial support.
Competing Interests: The authors declare that they have no conflict of interests.
Transparency: The authors confirm that the manuscript is an honest, accurate, and transparent account of the study was reported; that no vital features of the study have been omitted; and that any discrepancies from the study as planned have been explained.
Ethical: This study follows all ethical practices during writing. 
Publisher: Asian Online Journal Publishing Group

References

Aggraini, R. S., & Fuzan, A. (2018). The influence of realistic mathematics education (RME) approach on students' mathematical communication ability. Paper presented at the Advances in Social Science, Education, and Humanities Research (ASSEHR), 2nd International Conference on Mathematics and Mathematics Education 2018 (ICM2E 2018).

Andriani, L., & Fauzan, A. (2019). The impact of RME-based design instructional on students' mathematical communication ability. International Journal Of Scientific & Technology Research, 8(12), 2646-2649.

Chinh, P. D., Than, T., Doan, N. H., Hong, L. V., Thanh, T. C., & Thao, N. H. (2015). Mathematics 7, Bilingual Vietnamese-English. Vietnam: Vietnam Education Publishing House.

Deniz, O., & Kabael, T. (2017). Students' mathematization process of the concept of slope within the realistic mathematics education. Hacettepe University Journal of Education, 32(1), 123-142. Available at: https://doi.org/10.16986/HUJE.2016018796 .

Djokic, O. (2014). RME as a teaching approach – a case study of elementary geometry in Serbian innovative 4th-grade textbook. Paper presented at the International Conference on Mathematics Textbook Research and Development 2014 (ICMT 2014).

Drijvers, P., Kodde-Buitenhuis, H., & Doorman, M. (2019). Assessing mathematical thinking as part of curriculum reform in the Netherlands. Educational studies in mathematics, 102(3), 435-456. Available at: https://doi.org/10.1007/s10649-019-09905-7 .

Freudenthal, H. (1973). Mathematics as an educational task (pp. 1-680). Dordrecht: Reidel, Publisher: Springer Netherlands.

Gil, E., & Ben-Zvi, D. (2011). Explanations and context in the emergence of students' informal inferential reasoning. Mathematical Thinking and Learning, 13(1-2), 87-108. Available at: https://doi.org/10.1080/10986065.2011.538295 .

Gravemeijer, K. (1997). Instructional design for reform in mathematics education. In. M. Beishuizen, K.P.E. Gravemeijer & E.C.D.M.van Lieshout (Eds.). The Role of Contexts and Models in the Development of Mathematical Strategies and Procedures (pp. 13-34). Utrecht: Freudenthal Institute.

Gravemeijer, K., & Terwel, J. (2000). Hans Freudenthal, un matemático en didáctica y teoría curricular. Journal of Curriculum Studies, 32(6), 777-796. Available at: https://doi.org/10.1080/00220270050167170 .

Gravemeijer, K., & Doorman, M. (1999). Context problems in realistic mathematics education: A calculus course as an example. Educational Studies in Mathematics, 39(1), 111-129.

Habsah, F. (2017). Developing teaching material based on realistic mathematics and oriented to the mathematical reasoning and mathematical communication. Journal of Mathematics Education Research, 4(1), 43-55. Available at: https://dx.doi.org/10.21831/jrpm.v4i1.10199 .

Hasibuan, I. S., & Amry, Z. (2017). Differences of students mathematical communication ability between problems based learning, realistic mathematical education and inquiry learning in SMP Negeri 1 Labuhan Deli. IOSR Journal of Research & Method in Education (IOSR-JRME), 7(6), 54-60. Available at: https://dx.doi.org/10.9790/7388-0706015460 .

Indriani, N., & Julie, H. (2017). Developing learning trajectory on the circumference of a cycle with realistic mathematics education (RME). Paper presented at the AIP Conference Proceedings 1868, 050022.

Koparan, T. (2015). Difficulties in learning and teaching statistics: teacher views. International Journal of mathematical education in science and technology, 46(1), 94-104. Available at: https://doi.org/10.1080/0020739X.2014.941425 .

Laurens, T., Batlolona, F. A., Batlolona, J. R., & Leasa, M. (2017). How does realistic mathematics education (RME) improve students’ mathematics cognitive achievement? Eurasia Journal of Mathematics, Science and Technology Education, 14(2), 569-578. Available at: https://doi.org/10.12973/ejmste/76959 .

Lizzeth, N.-I., & Omar, C.-S. (2021). The impact of a didactic strategy using technology to strengthen the learning of mathematics. Journal of Education and e-Learning Research, 8(1), 90-96.

Loc, N. P., & Hao, M. H. (2016). Teaching mathematics based on "mathematization" of theory of Realistic Mathematics Education: A study of the linear function Y=Ax+B. The International Journal of Engineering and Science (IJES), 5(6), 20-23.

Loc, N. P., & Tien, N. T. T. (2020). Approach to realistic mathematics education in teaching mathematics: A case of cosine theorem – Geometry 10. International Journal Of Scientific & Technology Research, 9(4), 1173-1178.

Luthfi, B., & Suparman. (2019). Design of pop-up book based on realistic mathematics education to improving spatial ability students of class VIII. Jurnal Pendidikan Bitara UPSI, 12, 1-9. Available at: https://doi.org/10.37134/bitara.vol12.1.2019 .

Makonye, J. P. (2014). Teaching functions using a realistic mathematics education approach: A theoretical perspective. International Journal of Educational Sciences, 7(3), 653-662. Available at: https://doi.org/10.1080/09751122.2014.11890228 .

Meika, I., Suryadi, D., & Darhim. (2018). Students' errors in solving combinatorics problems observed from the characteristics of RME modeling. Paper presented at the IOP Conf. Series: Journal of Physics: Conf. Series.

Mulbar, U., & Zaki, A. (2018). Design of realistic mathematics education on elementary school students. Paper presented at the IOP Conf. Series: Journal of Physics: Conf. Series.

Mullis, I. V. S., Martin, M. O., Ruddock, G. J., O'Sullivan, C. Y., & Preuschof, C. (2011). TIMSS 2011 assessment frameworks (pp. 1-192). The United States: Publisher: TIMSS & PIRLS International Study Center Lynch School of Education, Boston College.

Palinussa, A. L. (2013). Students' critical mathematical thinking skills and character: experiments for junior high school students through realistic mathematics education culture-based. Indonesian Mathematical Society Journal on Mathematics Education, 4(1), 75-94.

Sumirattana, S., Makanong, A., & Thipkong, S. (2017). Using realistic mathematics education and the DAPIC problem-solving process to enhance secondary school students' mathematical literacy. Kasetsart Journal of Social Sciences, 38(3), 307-315. Available at: http://dx.doi.org/10.1016/j.kjss.2016.06.001.

Supriyanto, J. S., & Hairun, Y. (2020). Design of worksheets for RME model to Improve Mathematical communication. Universal Journal of Educational Research, 8(4), 1363-1371. Available at: http://dx.doi.org/10.13189/ujer.2020.080429.

Treffers, A. (1993). Wiskobas and freudenthal – realistic mathematics education. Educational Studies in Mathematics, 25(1-2), 89-108. Available at: https://doi.org/10.1007/bf01274104 .

Trisnawati, Pratiwib, R., & Waziana, W. (2018). The effect of realistic mathematics education on student's mathematical communication ability. Malikussaleh Journal of Mathematics Learning, 1(1), 31-35. Available at: https://doi.org/10.29103/mjml.v1i1.741 .

Trung, N. T., Thao, T. P., & Trung, T. (2019). Realistic mathematics education (RME) and didactical situations in mathematics (DSM) in the context of education reform in Vietnam. Paper presented at the IOP Conf. Series: Journal of Physics: Conf. Series 1340.

Uzel, D., & Uyangor, S. M. (2006). Attitudes of 7th class students toward mathematics in Realistic Mathematics Education. International Mathematical Forum, 1(39), 1951-1959.

Van Den Heuvel-Panhuizen, M. (2003). The didactical use of models in realistic mathematics education: An example from a longitudinal trajectory on percentage. Educational studies in mathematics, 54(1), 9-35. Available at: https://doi.org/10.1023/b:educ.0000005212.03219.dc .

Van den Heuvel-Panhuizen, M. (2000). Mathematics education in the Netherlands: A guided tour. Freudenthal Institute Cd-rom for ICME9. Utrecht: Utrecht University.

Van den Heuvel-Panhuizen, M., & Drijvers, P. (2014). Realistic mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 521–525). Dordrecht, Heidelberg, New York, London: Springer.

Wahyudi, Joharman, & Ngatman. (2017). The development of realistic Mathematics education (RME) for primary schools' prospective teachers. Advances in Social Science, Education, and Humanities Research (ASSEHR), International Conference on Teacher Training and Education 2017 (ICTTE 2017), 158, 814-826.

Webb, D. C., Van der Kooij, H., & Geist, M. R. (2011). Design research in the Netherlands: introducing logarithms using realistic mathematics education. Journal of Mathematics Education at Teachers College Spring–Summer 2011, 2, 47-52.

Widada, W., Herawaty, D., Yanti, D., & Izzawati, D. (2018). The student mathematical communication ability in learning ethnomathematics oriented realistic mathematics. International Journal of Science and Research (IJSR), 7(9), 881-884. Available at: https://doi.org/10.21275/ART20191277.

Yerizon, A., I.M., & Ismail, R. N. (2020). Improving student's mathematical communication skills through mathematics worksheet based on realistic mathematics education. International Journal of Advanced Research and Publications, 4(1), 42-46.

Yilmaz, R. (2020). Prospective mathematics teachers' cognitive competencies on realistic mathematics education. Journal on Mathematics Education, 11(1), 17-44. Available at: https://doi.org/10.22342/jme.11.1.8690 .

Yuanita, P., Zulnaidi, H., & Zakaria, E. (2018). The effectiveness of realistic Mathematics Education approach: The role of mathematical representation as a mediator between mathematical belief and problem-solving. PLoS ONE, 13(9), e0204847. Available at: https://doi.org/10.1371/journal.pone.0204847.

Asian Online Journal Publishing Group is not responsible or answerable for any loss, damage or liability, etc. caused in relation to/arising out of the use of the content. Any queries should be directed to the corresponding author of the article.