An Overview on Evaluation of E-Learning/Training Response Time Considering Artificial Neural Networks Modeling
1,2Computer Engineering Department, Al-Baha Private College of Sciences Al-Baha, (KSA)
3 Educational Psychology Department, Educational College Banha University, Egypt.
Abstract
The objective of this piece of research is to interpret and investigate systematically an observed brain functional phenomenon which associated with proceeding of e-learning processes. More specifically, this work addresses an interesting and challenging educational issue concerned with dynamical evaluation of e-learning performance considering convergence (response) time. That's based on an interdisciplinary recent approach named as Artificial Neural Networks (ANNs) modeling. Which incorporate Nero-physiology, educational psychology, cognitive, and learning sciences. Herein, adopted application of neural modeling results in realistic dynamical measurements of e-learners' response time performance parameter. Initially, it considers time evolution of learners' experienced acquired intelligence level during proceeding of learning / training process. In the context of neurobiological details, the state of synaptic connectivity pattern (weight vector) inside e-learner's brain-at any time instant-supposed to be presented as timely varying dependent parameter. The varying modified synaptic state expected to lead to obtain stored experience spontaneously as learner's output (answer). Obviously, obtained responsive learner's output is a resulting action to any arbitrary external input stimulus (question). So, as the initial brain state of synaptic connectivity pattern (vector) considered as pre-intelligence level measured parameter. Actually, obtained e-learner’s answer is compatibly consistent with modified state of internal / stored experienced level of intelligence. In other words, dynamical changes of brain synaptic pattern (weight vector) modify adaptively convergence time of learning processes, so as to reach desired answer. Additionally, introduced research work is motivated by some obtained results for performance evaluation of some neural system models concerned with convergence time of learning process. Moreover, this paper considers interpretation of interrelations among some other interesting results obtained by a set of previously published educational models. The interpretational evaluation and analysis for introduced models results in some applicable studies at educational field as well as medically promising treatment of learning disabilities. Finally, an interesting comparative analogy between performances of ANNs modeling versus Ant Colony System (ACS) optimization presented at the end of this paper.
Keywords: Artificial neural network modeling, E-Learning performance evaluation, Synaptic connectivity, Ant colony system.
1. Introduction
Due to currently rapid development in the learning field sciences, and technology-mediated learning, many educational experts adopted facing of recent educational systems' challenges (Hassan, 2005). Referring to (Grossberg, 1988) natural intelligence and artificial neural networks (ANNs) models have been adopted to investigate systematically mysteries of the most complex biological neural system (human brain). Accordingly, evolutionary interdisciplinary trends have been adopted by educationalists, neurobiologists, psychologists, as well as computer engineering researchers in order to carry out realistic investigations for critical challenging educational issues (Hassan, 1998); (Hassan, 2004); (Hassan, 2005b). Furthermore, during last decade of last century, educationalists have adopted recent Computer generation namely as natural intelligence as well as developed trends in information technology in to reach systematic analysis and evaluation of learning processes' performance phenomenon. In more details, it is worthy to refer to White House Ostp Report(U.S.A.) in 1989; therein, it has been announced that decade (1990-2000) named as Decade of the brain (OSTP, 1989). Consequently, human brain functions' modeling by using applications of artificial neural networks' paradigms have been considered as an adopted evolutional interdisciplinary approach by educationalists incorporating Nero-physiology, psychology, and cognitive learning sciences.
Generally, evaluation of learning performance is a challenging, interesting, and critical educational issues (Hassan, 2007); (Hassan, 2008).
Hassan (2016b); Hassan (2016c); Hassan (2014); Hassan (2012). Specifically, considering academic performance of e-learning systems some interesting papers have been published as introduced at Hassan (2011a); Hassan (2011b); Hassan (2011b); Hassan (2013); Hassan (2014); Hassan (2016c). Educationalists have been in need for knowing how neurons synapses inside the brain are interconnected together, and communication among brain regions (Swaminathan, 2007). By this information they can fully understand how the brain’s structure gives rise to perception, learning, and behavior, and consequently, they can investigate well the learning process phenomenon. This paper presents an investigational approach getting insight with e-learning evaluation issue adopting (ANNs) modeling. The suggested model motivated by synaptic connectivity dynamics of neuronal pattern(s) inside brain which equivalently called as synaptic plasticity while coincidence detection learning (Hebbian rule) is considered (Hebb, 1949). The presented interdisciplinary work aims to simulate appropriately performance evaluation issue in e-learning systems with special attention to face to face tutoring .That purpose fulfilled by adopting learner’s convergence (response) time ,(as an appropriate metric parameter) to evaluate his interaction with e-learning course material(s) . In fact this metric learning parameter is one of learning parameters recommended for using in educational field by most of educationalists. In practice, it is measured by a learner's elapsed time till accomplishment of a pre-assigned achievement level (learning output) (Hebb, 1949); (Hassan, 2005a); (Tsien, 2001). Thus, superior quality of evaluated e-leaning system performance could be reached via global decrement of learners' response time. Accordingly, that response time needed -to accomplish pre-assigned learners’ achievement- is a relevant indicator towards quality of any-under evaluation- learning system. Obviously, after successful timely updating of dynamical state vector (inside e-learner's brain) pre-assigned achievement is accomplished (Tsien, 2000); (Fukaya, 1988). Consequently, assigned learning output level is accomplished if and only if connectivity pattern dynamics (inside learner’s brain) reaches a stable convergence state,(following Hebbian learning rule). In other words, connectivity vector pattern associated to biological neuronal network performs coincidence detection to input stimulating vector. i.e. inside a learner's brain, dynamical changes of synaptic connectivity pattern (weight vector) modifies adaptively convergence time, so as to deliver (output desired answer). Hence, synaptic weight vector has become capable to spontaneous responding (delivering correctly coincident answer) to its environmental input vector (question) (Hebb, 1949); (Kandel, 1979); (Haykin, 1999); (Tsien, 2000); (Douglas, 2005). Interestingly, some innovative research work considering the analogy between learning at smart swarm intelligence (Ant Colony Systems) and that at behavioral neural have been published at Hassan (2008); Hassan (2008); Hassan (2008); Ursula (2008); Hassan (2015a); Hassan (2015b).
The rest of this paper is organized as follows. The next second section composed of two subsections (2.1 & 2.2). At subsection 2.1, revising for the two basic brain functions learning and memory is introduced in brief. The mathematical formulation for a single neuronal modeling function presented at subsection 2.2. At the third section, the analogy between brain functions and ANN models is illustrated. A review for performance evaluation techniques is given at the fourth section. Selectivity criteria in ANN models are briefly reviewed at the fifth section. At sixth section, modeling for three learning phases (Learning under supervision face to face), unsupervised learning (self-study), and learning by interaction with fellow learners) is presented . Experimental measurement of response time and simulation results are shown at the seventh section. This section considers the effect of gain factor of ANN on the time response in addition to comparative analogy between the gain factor effect- during learning process evaluation- in neural systems. Versus the impact of intercommunication cooperative learning cooperative learning parameter -while to solving Traveling Sale Man Problem - in Ant Colony System (ACS). At the last eighth section, some interesting conclusions and suggestions for future work are presented. Finally, by the end of this paper three Appendices are given .Appendices A&B illustrate the mathematical modeling equations given in the above considering learning (with and without supervision paradigms) respectively. They are written according to MATLAB software -version 6- programming language. The third Appendix C is presenting a simplified macro level flowchart describing algorithmic steps for different number of neurons using Artificial Neural Networks modeling.
2. Revising of Learners' Brain Function
2.1 Basic Brain Functions
Referring to OSTP REPORT (U.S.A.) in 1989 that announced Decade of the brain (1990-2000) (OSTP, 1989). The neural network theorists as well as neurobiologists have focused their attention on making a contribution to investigate systematically biological neural systems (such as the brain), functions. There is a strong belief that making such contribution could be accomplished by adopting recent direction of interdisciplinary research work, combining (ANNs) with neuroscience, by construction of biologically inspired artificial neural models it might have become possible to shed light on behavioral functions concerned with biological neural system.
Additionally, recent biological experimental findings have come to interesting results for evaluation of intelligent brain functions (Learning and memory) (Grossberg, 1988); (Freeman, 1994). However, about quarter of a century ago, in practical neuroscience experimental work carried out by many biologists declared results that even small systems of neurons are capable of forms of learning and memory (Kandel, 1979). It is well known that intelligence must emerge from the workings of the three-pound mass (brain) of wetware packed inside learners' skulls (Kandel, 1979). analytical conceptual study for human learning creativity observed at our classrooms is presented (Hassan, 2008). Also, learning creativity phenomenon is an interesting and challenging issue associated to educational practice. Moreover, that phenomenon is tightly related to main human brain functions (Learning and Memory) (Freeman, 1994); (Hassan, 2007). Due to the fact of human brain’s high neuronal density, humans have (in approximate)11.5 billion cortical neurons, which more than any other mammalian brains' neurons. Biological information processing capacity in a brain depends on how fast its nerves conduct electrical impulses. The most rapidly conducting nerves are swathed in sheaths of insulation called myelin. The thicker a nerve’s myelin sheath, the faster the neural impulses travel along that nerve. That information travels faster in the human brain than it does in non-primates' brains (Ursula, 2008); (Kandel, 1979).
Recently, the relation between number of neurons and information-processing capacity; and efficiency at hippocampus brain area of a mice is published at Hassan (2008). In addition, the effect of increasing number of neurons on learning response time (after a modified ANN model) is given at (APPENDIX B )
By some details about both features are tightly coupled to each other and they basically defined as follows (Hassan, 2007):
1) Learning: is the ability to modify behavior in response to stored experience (inside brain synaptic connections).
2) Memory: is that ability to store that modification (information) over a period of time as well as to retrieve spontaneously modified experienced (learned) patterns.
Moreover, some recently published work (based on neural network modeling) illustrated the tight mutual relation between learning and memory (Grossberg, 1988); (Freeman, 1994); (Hassan, 2007). Additionally, about one decade ago two other published articles have considered learning convergence time. They presented respectively: modeling of neural networks for evaluation of the effect of brain learners' ability, and the effect of learning under noisy environmental data and not well prepared instructors (Hassan, 2016a); (Ghonaimy et al., 1994a); (Ghonaimy et al., 1994b). Inside brain structure, synaptic connectivity patterns relies upon information processing conducted through communication between neuronal axonal outputs to synapses. Obviously, improvement of basic building blocks(neurons) function structure inevitably conduct significant enhancement of global brain function.
At Fig.1 , a single biological neuron is illustrated schematically .For more details concerned with the function of any biological neuron , the reader is recommended to review a comprehensive foundation reference (Haykin, 1999). Thus , enhancement of e-learners' intelligence (learning and memory) could be performed by enhancement of neuronal activation (response) function. Accordingly, the following subsection(2.2) presents a detailed mathematical formulation of a single neuron function.
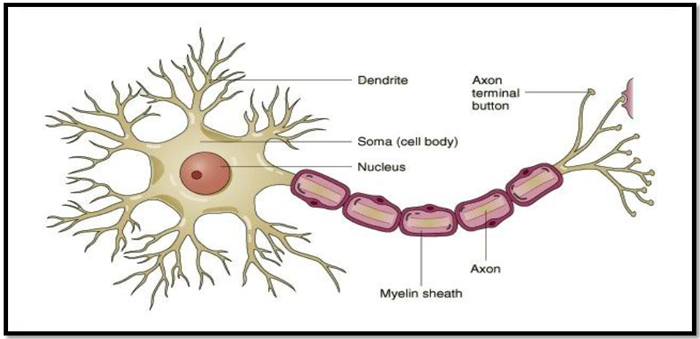
Fig-1. A simplified schematic illustration for a biological neuronal model (adapted from, Haykin (1999)).
2.2. Mathematical Formulation of a Single Neuronal Function
Referring to T.Kohenen’s two research works (Kohonen, 1993); (Kohonen, 1988) the output neuronal response signal observed to be developed following what so called membrane triggering time dependent equation. This equation is classified as a complex non-linear partial deferential. Its solution works to provide us with the physical description of a single cell (neuron) membrane activity. However, considering its simplified formula, which equation may contain about 24 process variable and 15 non-linear parameters. Following some more simplification of any neuron cell arguments, that differential equation describing electrical neural activity has been suggested, as follows:

Where,
yij represents the activity at the input (j) of neuron (i) ,
f(yij) indicates the effect of input on membrane potential,
j(zi) is nonlinear loss term combining leakage signals, saturation effects occurring at membrane in addition to the dead time till observing output activity signal.
The steady state solution of the above simplified differential equation (1), proved to be presented as transfer functions. Assuming, the linearity of synaptic control effect, the output response signal is given by the equation:

Where, the function f has two saturation limits, f may be linear above a threshold and zero below or linear within a range but flat above.
qi is the threshold (offset) parameter , and
wij synaptic weight coupling between two neuron (i) and (j).
Above function (fi) has been Specifically, recommended to obey odd sigmoid signal function presented by equation y(U) as follows:
y (u)=(1-e-λ(U-q))/(1+e-λ(U- q)) (3)
Where
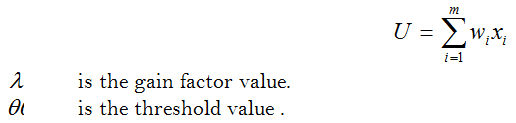
By referring, to the weight dynamics described by the famous Hebb’s learning law (Hassan, 2007) the adaptation process for synaptic interconnections is given by the following modified equation:
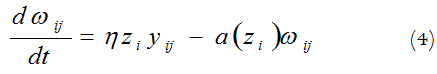
Where,
The first right term corresponds to the unmodified learning (Hebb’s law and h is the a positive constant representing learning rate value. The second term represents active forgetting, a(zi) is a scalar function of the output response (zi). The adaptation equation of the single stage model is as follows.
![]()
Where, the values of h , zi and yij are assumed all to be non-negative quantities (Freeman, 1994). The constant of proportionality h is less than one represents learning rate value, However a is a constant factor indicates forgetting of learnt output (Freeman, 1994) (it is also a less than one).
3. Brain Functions versus ANNS Modeling Performance
Development of neural network technology is originally motivated by computer scientists, educationalists, psychologists, and neurobiologists' interdisciplinary strong desire. That is to investigate realistic modeling of ANNS systems which implemented for contributing tasks similar to human brain functional performance. Basically such systems are characterized by their smartness (intelligence) and capabilities for performing intelligent tasks resembling experienced behaviors of human. Objectively, after a completing of training of well designed neural system models it is expected to respond correctly (in smart manner) and spontaneously towards input external stimuli. In brief, these systems well resemble human brain functionally in two ways:
1- Acquiring knowledge and experience through training / learning through adaptive weights neurodynamic.
2- Strong memorizing of acquired knowledge /stored experience within interconnectivities of neuronal synaptic weights.
The adopted neural model for simulation of learning performance evaluation follows the most common type of ANN. It is worthy to notice that by referring to the figure given in below (Fig.2), ten circles (4-3-3) represent three groups, or layers of biological neurons for four Inputs, three Hidden layer and one Output neuron. That is a Feed Forward Artificial Neural Network (FFANN) model consisted of units: a layer of "input" units is connected to a layer of "hidden" units, which is connected to a layer of "output" units. Obviously, any of such unit simulates a single biological neuron, which illustrated schematically in the above (Fig.1). Generally, the function of (FFANN) is briefly given as follows:
1-The activity of the input units represents the raw information that is fed into the network.
2-The activity of each hidden unit is determined by the activities of the input units and the weights on the connections between the input and the hidden units.
3-The behavior of the output units depends on the activity of the hidden units and the weights between the hidden and output units.
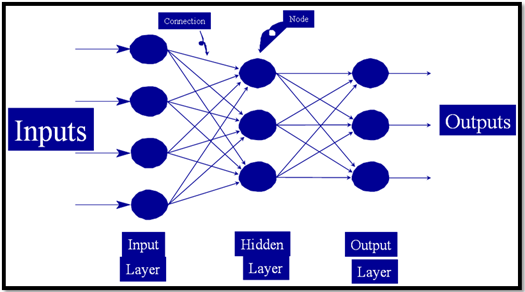
Fig-2. A simplified schematic diagram for a (FFANN) model (adapted from, Haykin (1999)).
Consequently, adopting of neural network modeling seems to be very relevant tool to perform simulation of educational activity phenomena. To implement realistically some simulated educational activities we should follow the advice that such models needed to be with close resemblance to biological neural systems. That resemblance ought to be not only from structural analysis but also from functional characterization. In other words understanding learning / training process carried out by ANN is highly recommended for increasing efficiency and effectiveness of any simulated educational activity. The statistical nature of training/learning time of convergence for a collection group (of ANN models) observed to be nearly Gaussian. This simulates a group of students under supervised learning. Additionally, the parameters of such Gaussian distribution (mean and variance) shown to be influenced by brain states of student groups as well as educational instrumental means. The well application of educational instrumentation during proceeding of learning/ training processes improves the quality of learning performance (learning rate factor). Such improvements are obtained in two folds. By better neurodynamic response of synaptic weights and by maximizing signal to noise ratio of input external learning data (input stimuli). So, any assigned learning output level is accomplished if and only if connectivity pattern dynamics (inside learner’s brain) reaches a stable convergence state. i.e. following Hebbian learning rule, connectivity vector pattern associated to biological neuronal network performs coincidence detection to input stimulating vector.
4. Performance Evaluation Techniques
The most widely used techniques for performance evaluation of complex computer systems are experimental measurement, analysis and statistical modeling, and simulation. Herein, all of three techniques are presented , with giving special attention to simulation using ANN modeling for learners' brain functions. Quantitative evaluation of timely updating brain function is critical for the delivery of a pre-assigned learning output level for a successful e-learning system. More precisely , inside a learner's brain , dynamical changes of synaptic connectivity pattern (weight vector) modifies adaptively convergence time, so as to deliver (output desired answer) .
4.1. Selecting an Appropriate Learning Parameter
Referring to some educational literature one of the evaluating parameter for learning processes is learning convergence time (equivalently as response time) (Haykin, 1999). By more details, at e-educational field practice while a learning processes proceeds, e-learners are affected naturally by technical characterizations as well as technological specifications of the interactive learning environment. Thus, learners have to submit their desired achievements (output learning levels) .Finally, by successive timely updated interaction with learning environmental conditions. This is well in agreement to the unsupervised (autonomous) learning paradigm following Hebbian rule (Hebb, 1949) in case of self-study learning. Conversely, considering the case of second learning way concerned with supervised learning (with a teacher) paradigm. It would be relevant to follow error correction learning algorithm as an ANN model (Haykin, 1999). Accordingly, two ANN models (supervised and unsupervised), are suggested for realistic simulation of both face to face learning ways :from tutor and from self-study, respectively (Al-Ajroush, 2004).
Accordingly, learners’ updated performance is directly (globally and/or individually) influenced by communication engineering efficiency of interactive channels. Such channels are practically non-ideal and contaminated by various types of noise sources accounting to some impairment to acquired learning data (Haykin, 1999). Of course, learning impairment accounts to worst learning performance with lower learning rate. Interestingly: poverty as a social phenomenon considered as environmental noise affecting learning reading (comprehension) performance. Moreover, the issue concerned with relation between noise effect and learning quality (measured by learning rate value) is discussed in details at research work (Hassan, 2016a). Obviously, various human/learning original phenomena such as Psychological, Cognitive styles, ……etc. , should have significant influence on learning environmental performance.
Conclusively, in practice; learning processes are virtually and/or actually vulnerable to non-ideal noisy data due to environmental conditions. Moreover, it is noticed learners' obtained achievements depends upon effectiveness of face to face tutoring process. Additionally, successful learners' interaction must emerge from the software quality of applied learning module packages. So , any assigned learning output level is accomplished if and only if connectivity pattern dynamics (inside learner's brain) reaches a stable convergence state. Accordingly, response time needed to accomplish pre-assigned learners’ achievement is a relevant indicator towards quality of any under evaluation system. Obviously, after successful timely updating of dynamical state vector (inside e-learner's brain) pre-assigned achievement is accomplished. Consequently, assigned learning output level is accomplished if and only if connectivity pattern dynamics (inside learner’s brain) reaches a stable convergence state (following Hebbian learning rule). In other words, connectivity vector pattern associated to biological neuronal network performs coincidence detection to input stimulating vector. i.e. inside a learner's brain, dynamical changes of synaptic connectivity pattern (weight vector) modifies adaptively convergence time, so as to deliver (output desired answer) .
4.2. Examinations in E-Learning Systems
In fulfillment of an e-learning system performance evaluation, time response parameter applied to measure any of e-learners’ achievement. Thus e-learner has to subject to some timely measuring examination that is composed as Multi choice questions. Hence, this adopted examination discipline is obviously dependent upon learners’ capability in performing selectivity of correct answer to questions they received. Consequently, to accomplish a pre-assigned achievement level, stored experience inside learner’s brain should be able to develop correct answer up to desired (assigned) level. In the context of biological sciences, selectivity function proceeds (during examination time period) to get on either correct or wrong answer to received questions spontaneously.
Accordingly, the argument of selectivity function is considered virtually as the synaptic pattern vector (inside brain) is modified to post training status. Hence, selected answer results in synaptic weight vector has become capable to respond spontaneously (delivering correctly coincident answer) to its environmental input vector (question) (Fukaya, 1988); (Haykin, 1999).
5. Selectivity Criteria
Referring to adopted performance evaluation technique of e-learning systems by response time parameter. Accomplishment of a learner’s output is dependent on the optimum selection of correct answer as quick as possible. So it is well relevant to present ANN models that capable to perform selectivity function while solving some critical problems. Consequently, the goal of this section is that to give -in brief- an overview over mathematical formulations of selectivity criteria adopted by various neural network models. This overview sheds light on the selectivity criterion adopted by our proposed model. Presented selectivity criteria are given in a simplified manner for four neural network models adopting adaptive selectivity criterion, as follows:
5.1. Selectivity Criterion by Grandmother Models (Caudill, 1989)
On the basis of grandmother modelling, a simple sorting system has been constructed using a set of grandmother cells. That implies, each neuron has been trained in order to respond exactly to one particular input pattern. In other words, each neuron has become able (after training) to recognize its own grandmother. Appling such models in real world, they have been characterized by two features. Firstly, a lot number of grandmother cells are required to implement such grandmother model. That is due to the fact each cell is dedicated to recognize only one pattern. Secondly, it is needed to train that simple sorting network possible grandmother pattern to obtain correct output response. Consequently, all synaptic weight values at this model have to be held up unchanged (fixed weights). Hence, it is inevitably required to either add new grandmother cell(s),to recognise additional new patterns or, to modify weights of one or more existing cells to recognise that new patters.
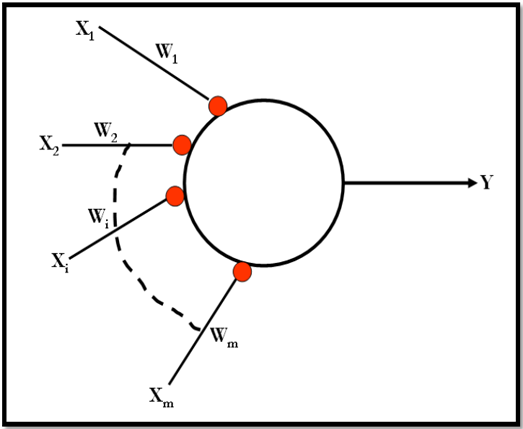
Fig-3. Illustrates a single grandmother cell (artificial neuronal cell) that works as processing element. (Adapted from (Caudill, 1989))
The above grandmother model could be described well by following mathematical formulation approach.
The output of any grandmother cell (neuron) is a quantizing function defined as follows:
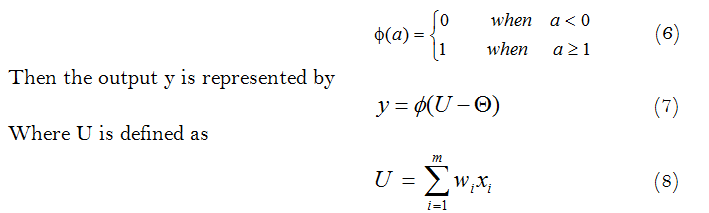
That model utilizes a set of grandmother neuronal cells (nodes). Each of these nodes responds exactly to only one particular input data vector pattern. Therefore, for some specific input vector pattern with m dimension is needed to make only one of model nodes to fire selectively to it.
5.2. Kohonen’s Selectivity Criterion (Kohonen, 1993); (Kohonen, 2002)
The most famous approach of neuronal modelling based on selectivity is proposed by T.Kohonen and applied for Self Organizing Map (SOM) (Kohonen, 1993). The SOM is based on vector input data to Kohonen neuronal model. That input is a vector data pattern developed as to change the status of the model. The changes are based on incremental stepwise correction process. The original algorithm of SOM aims to determine what so called winner take all (WTA) function. That function is referred to some physiological selectivity criterion applied as to define initially the function C that to search for mi(t) to be closest to x(t)
![]()
where x(t) is an n-dimensional vector data as one input sample, and mi(t) is a spatially ordered set of vector models arranged as a grid, and t is a running index of input samples and also index of iteration steps. The iterative process supposed to be continuous by time ![]() as to obtain the asymptotic values of the mi constitute the desired ordered projection at the grid.
as to obtain the asymptotic values of the mi constitute the desired ordered projection at the grid.
5.3. Hopfield Network Selectivity Model (Haykin, 1999)
It is proved to be closely attached with that network computational power. To obtain decisions in some optimisation problems, the computational power is demonstrated by the Hopfield NN model selectivity. That, it means the ability to select one of possible answers that model might give. Therein, resulting selectivity pattern (for all possible solutions) shown in a form of histogram. As numerical example, the value of selectivity of Hopfield neural network model was about 10-4 – 10-5. That when it is applied to solve travelling salesman problem (TSP) considering 100 neurons. That given value of selectivity is the fraction of all possible solutions. In practice, it is noticeable that by increasing number of neurons comprising Hopfield network, selectivity of the network expected to be better (increased). The cost function concept supports the above presented selectivity criterion in TSP. By referring to Eq. (6) given at subsection (5.1), pattern of vector pairs are x andy the model are respectively called key and stored patterns of vectors . The concept of cost function is adopted as to measure of how far away we are from optimal solution of memorization problem. Proposed mathematically, illustrations of cost is a function of observations and the problem becomes that to find the model f which minimises C value
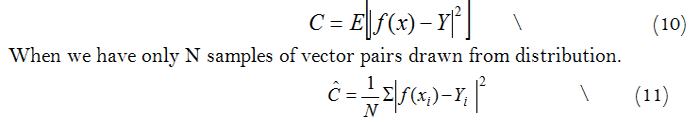
5.4. Selectivity Criterion for Learning by Interaction with Environment (Fukaya, 1988)
It is worthy to note that selectivity condition considers a network model adopting artificial neurons with threshold (step) activation function as shown in the above at Fig.3.
The necessary and sufficient condition for some neuron to fire selectively to a particular input data vector (pattern) is formulated mathematically as given in below.
Consider the particular input pattern vector

6. Modeling E-Learning Performance
Fig-4. A general view for interactive educational process presenting face to face Interaction
6.1. Modeling of Face to Face Tutoring (Al-Ajroush, 2004)
In face to face tutoring , the phase of interactive cooperative learning is an essential paradigm aiming to improve any of e-Learning Systems' performance. In more details, face to face tutoring proceeds with three phases (Learning from tutor, Learning from self-study, and Learning from interaction with fellow learners). it has been declared that cooperative interactive learning among e-learning followers (studying agents learners).That phase contributes about one fourth of e-learning academic achievement (output) attained during face to face tutoring sessions (Al-Ajroush, 2004). At next subsection two phases concerned with the first and second phases are molded by one block diagram. However two diversified mathematical equations are describing the two phases separately. At the next subsection cooperative learning is briefly presented by referring to Ant Colony System (ACS) Optimization.
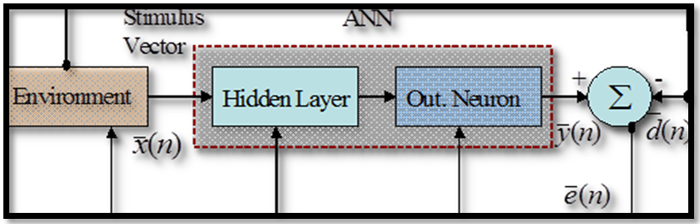
Fig-5. Block diagram for learning paradigm adopted for quantifying creativity adapted from Haykin (1999).
The error vector at any time instant (n) observed during learning processes is given by:

Vk(n)=Xj(n) WTkj(n) (15)
yk(n)=j(Vk(n))=1/(1+e-λvk(n)) (16)
ek(n)=|dk(n)-yk(n)| (17)
Wkj(n+1)=Wkj(n)+DWkj(n) (18)
Where: X input vector, W weight vector, j is the activation function, y is the output, ek the error value, and dk is the desired output. Noting that DWkj(n) the dynamical change of weight vector value.
The above four equations are commonly applied for both learning phases, supervised (Learning from tutor), and unsupervised (Learning from self-study). The dynamical change of weight vector value specifically for supervised phase is given by equation:
DWkj(n)=h ek(n) xj(n) (19)
Where h is the learning rate value during learning process for both learning phases. However, for unsupervised paradigm, dynamical change of weight vector value is given by equation:
DWkj(n)=h yk(n) xj(n) (20)
6.2. Gain Factor versus Learning Convergence
Referring to Hassan (2016a); Hassan (2014) learning by coincidence detection is considered. Therein, angle between training weight vector and an input vector have to be detected. Referring to Freeman (1994) the results of output learning processes considering Hebbian rule are following the equation:

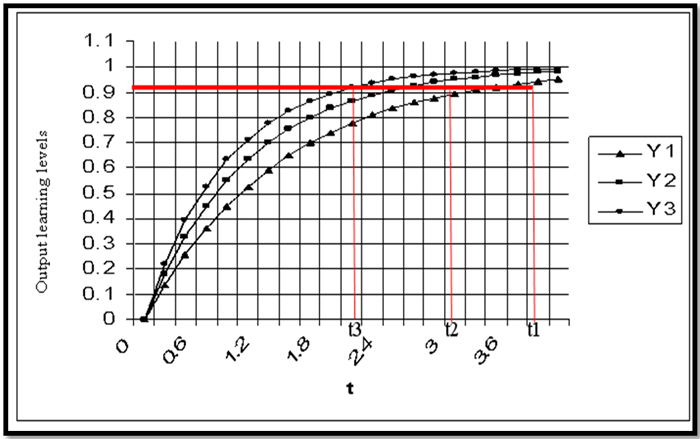
Fig-6. Illustrates three different learning performance curves Y1&Y2 and Y3 that converge at time t1&t2 ,and t3 considering different gain factor values 1 & 2 ,and 3. adapted from Freeman (1994).
Referring to Fig.6; the three curves shown represent different individual levels of learning. Curve (Y2) is the equalized representation of both forgetting and learning factors (Freeman, 1994). However curve (Y1) shown the low level of learning rate (learning disability) that indicates the state of angle between synaptic weight vector and an input vector . Conversely, the curve (Y3) indicates better learning performance that exceeds the normal level of learning at curve (Y2). Consequently learning time convergence decreases as shown at Fig.6, (t1& t2, and t3) three different levels of learning performance curves representing: normal, low, and better cases shown at curves Y1&Y2 and Y3 respectively.
7. Simulation Results
7.1. Gain Factor Values versus Response Time
The graphical simulation results illustrated in the below Figure 7, gain factor effect on improving the value of time response measured after learning process convergence, Hassan (2004). These four graphs at Fig.7 are concerned with the improvement of the learning parameter response time (number of training cycles). That improvement observed by increasing of gain factor values (0.5, 1, 10,and 20) that corresponds to decreasing respectively number of training cycles by values (10,7.7,5,and3) cycles, (on approximate averages).
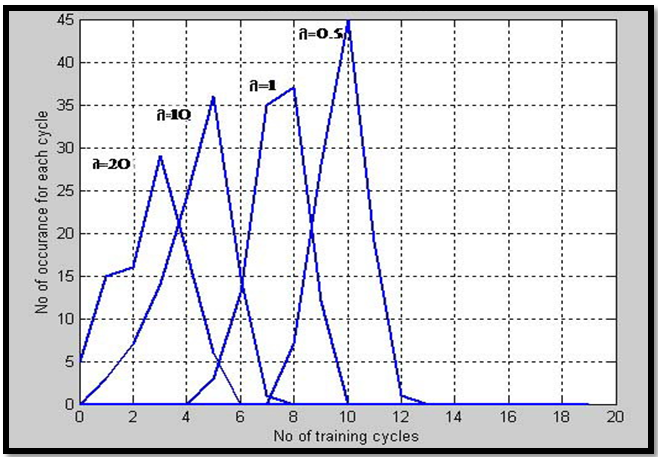
Fig-7. Illustrates improvement of average response time (no. of training cycles) by increase of the gain factor values.
7.2. Effect of Neurons' Number on Time Response
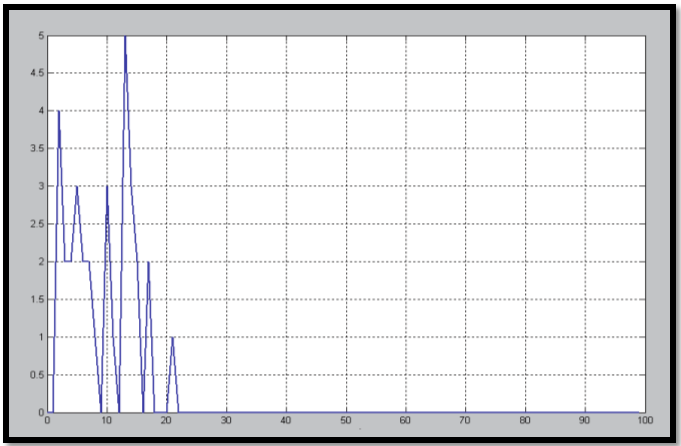
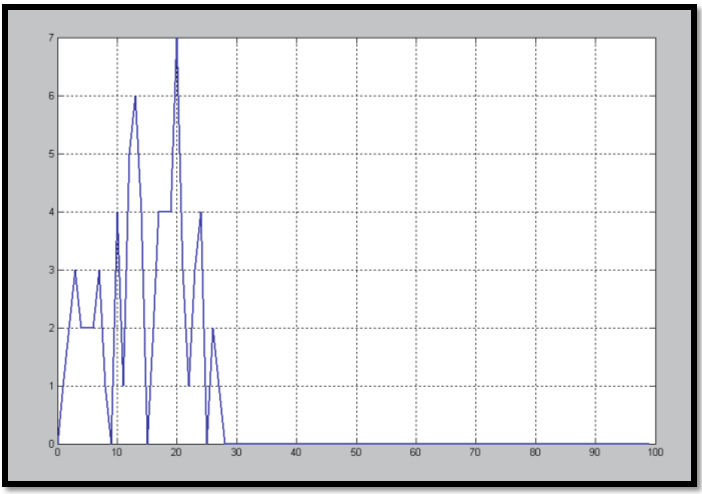
The following simulation results show how the number of neurons may affect the time response performance. Those graphical presented results show that by variation of neural cells' numbers (14 ,11 ,7 ,5 ,and 3 ); during interaction of students with e-learning environment, the performance observed to be improved well by increasing of neuronal cells' number (neurons).That improvement is observed by Figures: (8 , 9, 10, 11, 12) respectively; considering fixed learning rate = 0.1 and gain factor = 0.5.
In more details, these five figures have been depicted from the reference source : Hassan, M. H."On performance evaluation of brain based learning processes using neural networks," published at 2012 IEEE Symposium on Computers and Communications (ISCC), pp. 000672-000679, 2012 IEEE Symposium on Computers and Communications (ISCC), 2012. Available online at : http://www.computer.org/csdl/proceedings/iscc/2012/2712/00/IS264-abs.html
No. of occurrences for each Time
Time (No. of training cycles)
Figure-8. Considering # neurons= 14
No. of occurrences for each Time
Time (No. of training cycles)
Figure-9. Considering # neurons= 11
No. of occurrences for each Time
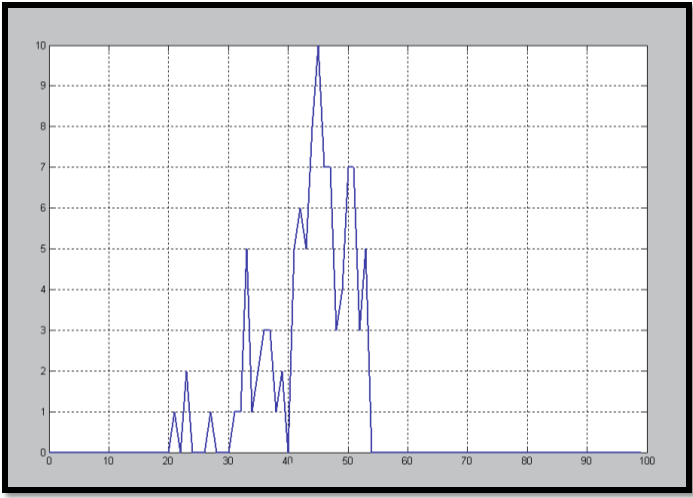
Time (No. of training cycles)
Figure-10. Considering # neurons= 7
No. of occurrences for each Time

Time (No. of training cycles)
Figure-11. Considering # neurons= 5
No. of occurrences for each Time
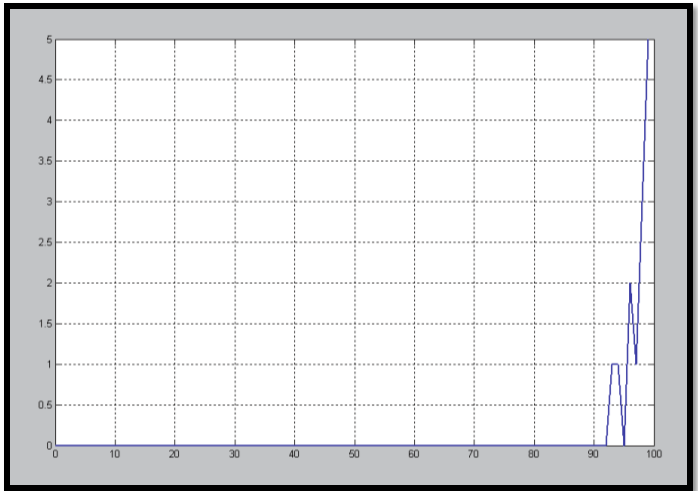
Time (No. of training cycles)
Figure-12. Considering # neurons= 3
7.3. Analogy of Behavioral Learning versus Cooperative Learning By ACS
Cooperative learning by Ant Colony System for solving TSP referring to Figure 13 which adapted from Dorigo and Gambardella (1997) the difference between communication levels among agents (ants) develops different outputs average speed to optimum solution. The changes of communication level are analogues to different values of λ in odd sigmoid function as shown at equation (24) in below.. When the number of training cycles increases virtually to an infinite value, the number of salivation drops obviously reach a saturation value additionally the pairing stimulus develops the learning process turned in accordance with Hebbian learning rule (Hebb, 1949). However in case of different values of λ other than zero implicitly means that output signal is developed by neuron motors. Furthermore, by increasing of number of neurons which analogous to number of ant agents results in better learning performance for reaching accurate solution as graphically illustrated for fixed λ at Figure 14 (Rechardson, 2006); (Bonabeau, 2001)
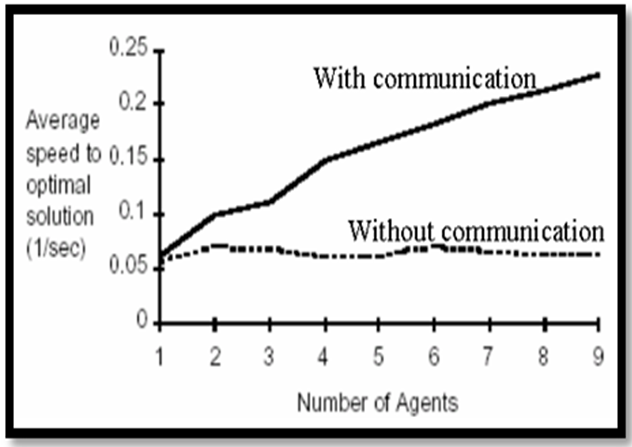
Figure-13. Illustrates performance of ACS with and without communication between ants.
The source is Dorigo and Gambardella (1997).
This different response speed to reach solution is analogous to different communication levels among agents (artificial ants) as shown at the Fig.10. It is worthy to note that communication among agents of artificial ants model develops different speed values to obtain an optimum solution of TSP, considering variable number of agents (ants).
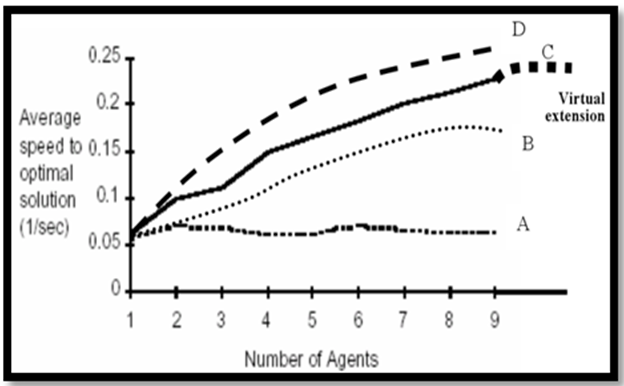
Fig-14. Communication determines a synergistic effect with different communication levels among agents leads to different values of average speed.
Consequently as this set of curves reaches different normalized optimum speed to get TSP solution (either virtually or actually) the solution is obtained by different number of ants, so this set could be mathematically formulated by following formula:

Where α……. is an amplification factors representing asymptotic value for maximum average speed to get optimized solutions and λ in the gain factor changing in accordance with communication between ants.
Referring to the figure -- in below, the relation between number of neurons and the obtained achievement is given considering three different gain factor values (0.5 , 1 ,and 2)
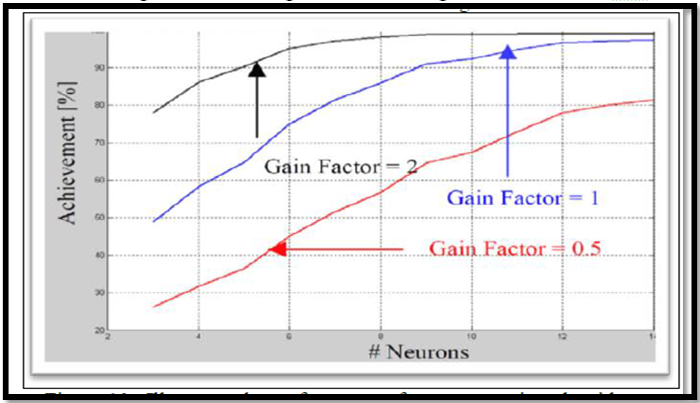
Fig-15. Illustrate students' learning achievement for different gain factors and intrinsically various number of neurons which measured for constant learning rate value = 0.3.
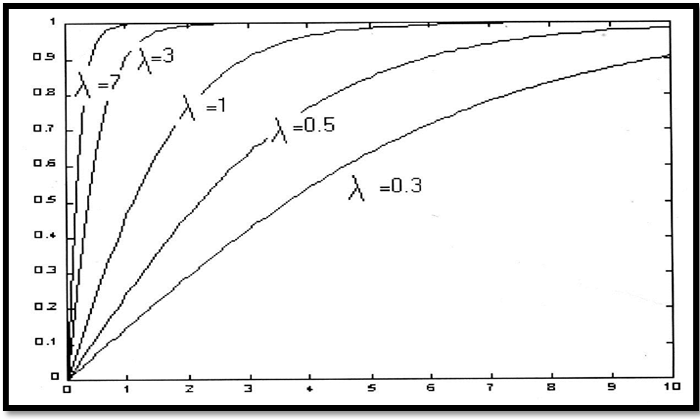
However by this mathematical formulation of that model normalized behavior it is shown that by changing of communication levels (represented by λ) that causes changing of the speeds for reaching optimum solutions. In given Fig. 16. in blow, it is illustrated that normalized model behavior according to following equation.
y(n)= (1-exp(-li(n-1)))/ (1+exp(-li(n-1))) (24)
where λi represents one of gain factors (slopes) for sigmoid function.
Normalized Output [y(n)]
Number of Training Cycles(n)
Fig-16. Graphical representation of learning performance of model with different gain factor values (λ)
8. Conclusions & Future Work
Herein, some conclusive remarks related to the obtained results are presented as well as some expected relevant future research directions that is carried out considering the effect of internal (intrinsic) learners' brain state as well as external environmental factors upon convergence of learning / training processes.
8.1. Conclusions
Through above presented performance evaluation approach, three interesting points are concluded subsequently to enhance quality of e-learning systems as follows:
1- Evaluation of any e-learning system's quality following previously suggested measurement of learning convergence/response time. The experimental measured average of response time values (quantified evaluation), provides educationalists with a fair and unbiased judgment for any e-learning system (considering a pre-assigned achievement level).
2- As consequence of above remark, relative quality comparison between two e-learning systems (on the bases of suggested metric measuring) is contributed by quantified performance evaluation.
3- modification of learning systems performance obtained by increment of learning rate value, which is expressed by the ratio between achievement level (testing mark) and the response learning time. This implies that learning rate could be considered as a modifying parameter contributes to both learning parameters (learning achievement level and learning convergence time response).
8.2. Future Research Work
The following are some research work directions that may be adopted in the future :
- Application of improved synaptic connectivity with random weight values in order to perform medically promising treatment of mentally disable learners.
- Simulation and modeling of complex educational issues such as deterioration of achievement levels at different learning systems due to non well prepared tutor .
- Study of ordering of teaching curriculum simulated as input data vector to neural systems. That improved both of learning and memory for the introduced simulated ANN model.
- Experimental measurement of learning systems' performance in addition to analytical modeling and simulation of these systems aiming to improve their quality.
Finally, more elaborate evaluation and assessment of individual differences phenomena that is needed critically for educational process.
References
Al-Ajroush, H., 2004. Associate manual for learners' support in face to face tuition. Arab Open University (KSA).
Bonabeau, 2001. Swarm smarts. Majallat Aloloom, 17(5): 4-12.
Caudill, M., 1989. Neural networks primer. San Francisco, CA: Miller Freeman Publications.
Dorigo, M. and L.M. Gambardella, 1997. Ant colony system: A cooperative learning approach to the travelling salesman problem. IEEE Transactions on Evolutionary Computation, 1(1): 53–66. View at Google Scholar | View at Publisher
Douglas, F.M.R., 2005. Making memories sticks. Majallat Aloloom, 21(3/ 4): 18-25.
Freeman, A.J., 1994. Simulating neural networks with mathematica. Addison-Wesley Publishing Company.
Fukaya, M., 1988. Two level neural networks: Learning by interaction with environment. 1st Edn., San Diego: ICNN.
Ghonaimy, M.A., A.M. Al- Bassiouni and H.M. Hassan, 1994a. Learning ability in neural network model. Second International Conference on Artificial Intelligence Applications, Cairo, Egypt, 400- 413, Jan (1994). pp: 22- 24.
Ghonaimy, M.A., A.M. Al- Bassiouni and H.M. Hassan, 1994b. Learning of neural networks using noisy data. Second International Conference on Artificial Intelligence Applications, Cairo, Egypt, 400- 413, Jan (1994). pp: 22- 24.
Grossberg, S., 1988. Neural networks and natural intelligence. The MIT press. pp: 1-5.
Hassan, 2011a. Building up bridges for natural inspired computational models across behavioral brain functional phenomena; and open learning systems. A Tutorial Presented at the International Conference on Digital Information and Communication Technology and its Applications (DICTAP2011) which held from June 21-23, 2011 , at Universite de Bourgogne, Dijon, France.
Hassan, 2011b. Natural inspired computational models for open learning. Published at the 5th Guide International Conference held in Rome (Italy) 18 - 19 November 2011.
Hassan, 2012. On performance evaluation of brain based learning processes using neural networks. Published at 2012 IEEE Symposium on Computers and Communications (ISCC), 2012 IEEE Symposium on Computers and Communications (ISCC), 2012. pp: 000672-000679.
Hassan, 2013. On optimal analysis and evaluation of time response in e-learning systems (Neural Networks Approach) .Published at EDULEARN13, the 5th annual International Conference on Education and New Learning Technologies which will be held in Barcelona (Spain), on the 1st, 2nd and 3rd of July, 2013.
Hassan, 2014. Optimal estimation of penalty value for on line multiple choice questions using simulation of neural networks and virtual students' testing. Published at the Proceeding of UKSim-AMSS 16th International Conference on Modeling and Simulation held at Cambridge University (Emmanuel College),on 26-28 March 2014.
Hassan, 2016a. An overview on classrooms' academic performance considering: Non-properly prepared Instructors, Noisy learning environment, and overcrowded classes (Neural Networks' Approach)" has been accepted for oral presentation and publication at the upcoming 2015 6th International Conference on Distance Learning and Education (ICDLE 2015).
Hassan, 2016b. On comparative analysis and evaluation of teaching how to read arabic language using computer based instructional learning module versus conventional teaching methodology using neural networks' modeling (With A Case Study)" has been accepted to be published at the Innovation Arabia 9 organized by Hamdan Bin Mohammed Smart University. The Conference held at Jumeirah Beach Hotel - Dubai, UAE| from 7 - 9 March 2016.
Hassan, H.M., 1998. Application of neural network model for analysis and evaluation of students individual differences. Proceeding on the 1st ICEENG Conference (MTC) Cairo, Egypt. pp: 24-26.
Hassan, H.M., 2004. Evaluation of learning/training convergence time using neural network (ANNs). Published at International Conference of Electrical Engineering. M.T.C.,Cairo, Egypt on 24-26 Nov. 2004. pp: 542-549.
Hassan, H.M., 2005a. On simulation of adaptive learner control considering students' cognitive styles using artificial neural networks (ANNs). Austria: Published at CIMCA.
Hassan, H.M., 2005b. Statistical analysis of individual differences in learning/teaching phenomenon using artificial neural networks ANNs modeling. With a case study. Delhi, India: Published at ICCS.
Hassan, H.M., 2007. Evaluation of memorization brain function using a spatio-temporal artificial neural network (ANN) model. Published at CCCT 2007 Conference held on July12-15 ,2007 – Orlando, Florida, USA.
Hassan, H.M., 2008. On comparison between swarm intelligence optimization and behavioral learning concepts using artificial neural networks (An Over View). Published at the 12th World Multi-Conference on Systemics, Cybernetics and Informatics: WMSCI 2008 The 14th International Conference on Information Systems Analysis and Synthesis: ISAS 2008 June 29th - July 2nd, 2008 – Orlando, Florida, USA.
Hassan, H.M., 2008. A comparative analogy of quantified learning creativity in humans versus behavioral learning performance in animals: Cats, dogs, ants, and rats. (A Conceptual Overview). to be Published at WSSEC08 Conference to be held on 18-22 August 2008, Derry, Northern Ireland.
Hassan, H.M., 2008. On analysis of quantifying learning creativity phenomenon considering brain synaptic plasticity. Published at WSSEC08 Conference to be held on 18-22 August 2008, Derry, Northern Ireland.
Hassan, H.M., 2014. Dynamical evaluation of academic performance in e-learning systems using neural networks modeling (Time Response Approach). Published at IEEE EDUCON - Engineering Education 2014 held in Istanbul Turkey. Retrieved from http://ieeexplore.ieee.org/xpl/abstractAuthors.jsp?arnumber=6826150 [Accessed 3-5 of April, 2014].
Hassan, H.M., 2015a. Comparative performance analysis for selected behavioral learning systems versus ant colony system performance (Neural Network Approach). Published at the International Conference on Machine Intelligence ICMI 2015.Held on Jan 26-27, 2015, in Jeddah, Saudi Arabia.
Hassan, H.M., 2015b. Comparative performance analysis and evaluation for one selected behavioral learning system versus an ant colony optimization system. Published at the Proceedings of the Second International Conference on Electrical, Electronics, Computer Engineering and their Applications (EECEA2015), Manila, Philippines, on Feb. 12-14, 2015.
Hassan, H.M., 2016c. On brain based modeling of blended learning performance regarding learners' self-assessment scores using neural networks (Brain Based Approach). Published at IABL 2016:The IABL Conference International Association for Blended Learning (IABL) will be held in Kavala Greece on 22-24 April 2016.
Hassan, M.H., 2005. On quantitative mathematical evaluation of long term potentation and depression phenomena using neural network modeling. Published at SIMMOD, 17- 19 Jan. 2005. pp: 237- 241.
Haykin, S., 1999. Neural networks. Englewood Cliffs, NJ: Prentice-Hall.
Hebb, D.O., 1949. The organization of behavior, a neuropsychological theory. New York: Wiley.
Kandel, E.R., 1979. Small systems of neurons. Scientific American, 241(3): 66-76.
Kohonen, T., 1988. State of the art in neural computing. 2nd ICNN.
Kohonen, T., 1993. Physiological interpretation of the self organizing map algorithm. Neural Networks, 6(6): 895- 909.View at Google Scholar | View at Publisher
Kohonen, T., 2002. Overture, self- organizing Neural Networks, re cent advances and applications. U. Seifert an Jain, L. C. (Eds.). New York: Physica- Verlag Heidelberg.
OSTP, 1989. White House OSTP Issues Decade of the Brain Report, Maximizing Human Potential: 1990-2000.
Rechardson, 2006. Teaching in tandem-running ants. Nature, 439(7073): 153-153.View at Google Scholar
Swaminathan, N., 2007. Cognitive ability mostly developed before adolescence, NIH study says. NIH Announces Preliminary Findings from an Effort to Create a Database that Charts Healthy Brain Growth and Behavior Scientific American letter, May 18, 2007.
Tsien, J.Z., 2000. Linking Hebb’s coincidence-detection to memory formation. Current Opinion in Neurobiology, 10(2): 266-273. View at Google Scholar | View at Publisher
Tsien, J.Z., 2001. Building a brainier mouse. Scientific American, Majallat Aloloom, 17(5): 28- 35.
Ursula, D., 2008. Animal intelligence and the evolution of the human mind. Scientific American.